OpenGL Projection Matrix
Related Topics: OpenGL Transformation
Overview
A computer monitor is a 2D surface. We need to transform 3D scene into 2D image in order to display it. GL_PROJECTION matrix is for this projection transformation . This matrix is used for converting from the eye coordinates to the clip coordinates. Then, this clip coordinates are also transformed to the normalized device coordinates (NDC) by divided with w component of the clip coordinates.
Therefore, we have to keep in mind that both clipping and NDC transformations are integrated into GL_PROJECTION matrix. The following sections describe how to build the projection matrix from 6 parameters; left , right , bottom , top , near and far boundary values.
Perspective Projection
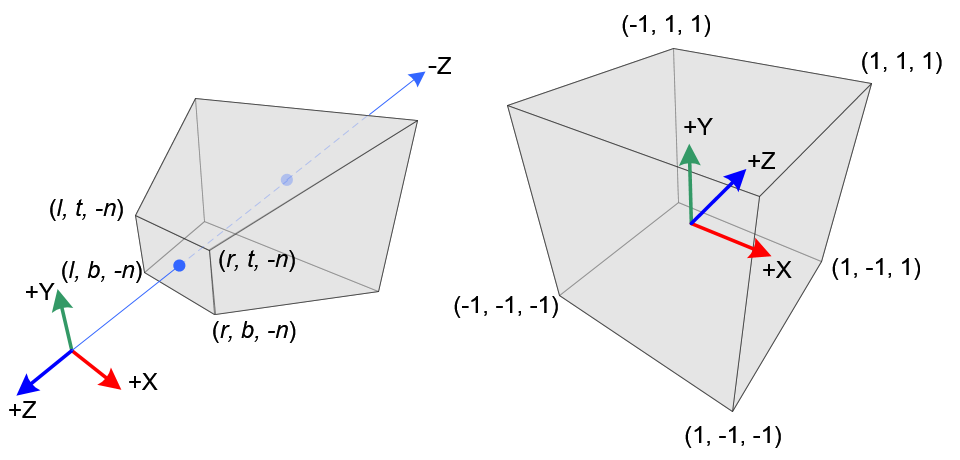 Perspective Frustum and Normalized Device Coordinates (NDC)
Perspective Frustum and Normalized Device Coordinates (NDC)
In perspective projection, a 3D point in a truncated pyramid frustum (eye coordinates) is mapped to a cube (NDC); the x-coordinate from [l, r] to [-1, 1], the y-coordinate from [b, t] to [-1, 1] and the z-coordinate from [n, f] to [-1, 1].
Note that the eye coordinates are defined in right-handed coordinate system, but NDC uses left-handed coordinate system. That is, the camera at the origin is looking along -Z axis in eye space, but it is looking along +Z axis in NDC. Since glFrustum() accepts only positive values of near and far distances, we need to negate them during construction of GL_PROJECTION matrix.
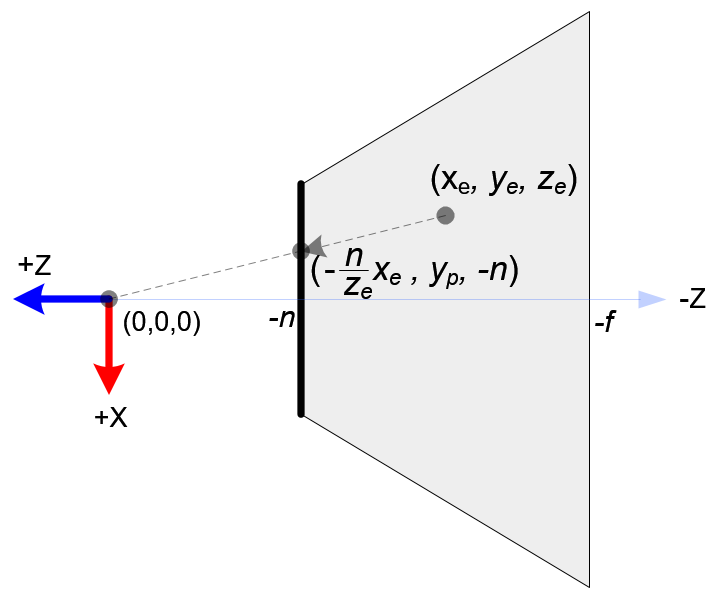
In OpenGL, a 3D point in eye space is projected onto the near plane (projection plane). The following diagrams shows how a point (xe , ye , ze ) in eye space is projected to (xp , yp , zp ) on the near plane.
 Top View of Projection
Top View of Projection
 Side View of Projection
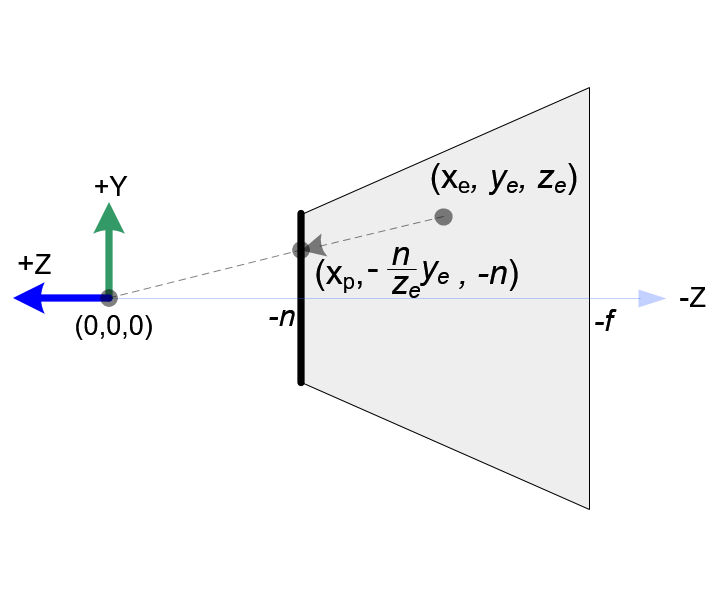
Side View of Projection
From the top view of the projection, the x-coordinate of eye space, xe is mapped to xp , which is calculated by using the ratio of similar triangles;
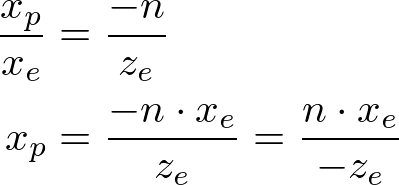
From the side view of the projection, yp is also calculated in a similar way;
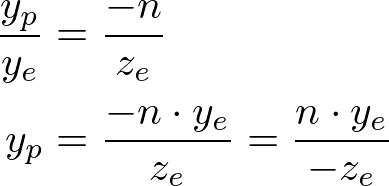
Note that both xp and yp depend on ze ; they are inversely propotional to -ze . It is an important fact to construct GL_PROJECTION matrix. After an eye coordinates are transformed by multiplying GL_PROJECTION matrix, the clip coordinates are still a homogeneous coordinates . It finally becomes normalized device coordinates (NDC) divided by the w-component of the clip coordinates. (See more details on OpenGL Transformation . )
 ,
, 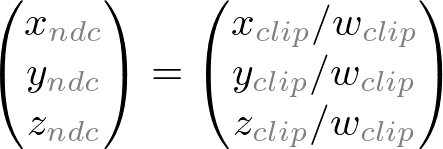
Therefore, we can set the w-component of the clip coordinates as -ze . And, the 4th of GL_PROJECTION matrix becomes (0, 0, -1, 0).
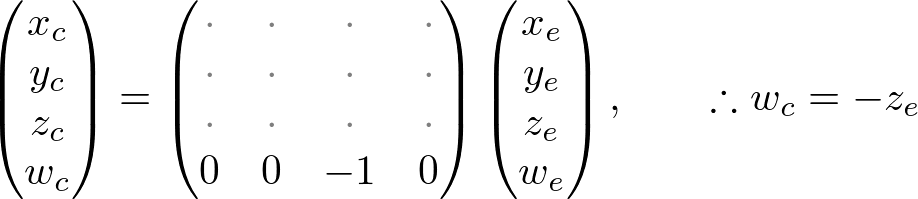
Next, we map xp and yp to xn and yn of NDC with linear relationship; [l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1].
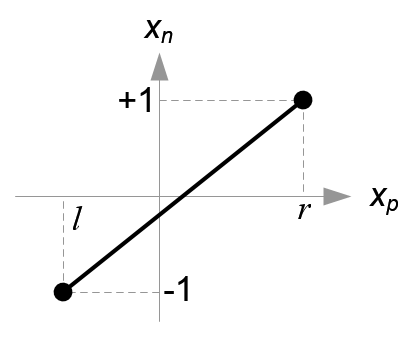 Mapping from xp to xn
Mapping from xp to xn
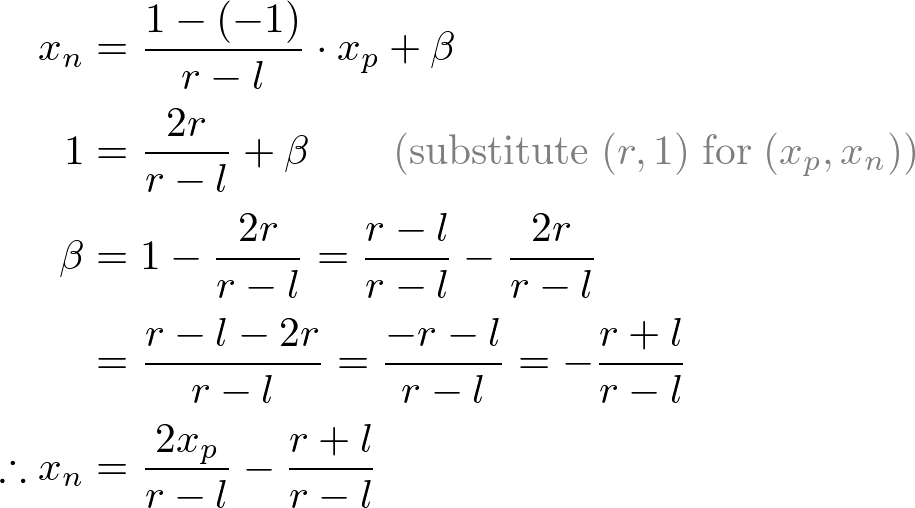
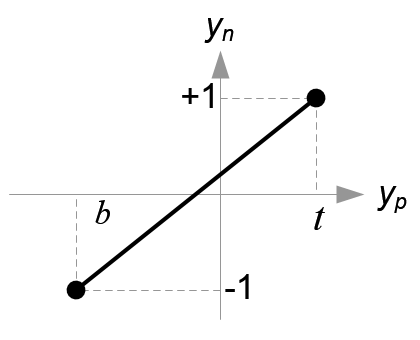 Mapping from yp to yn
Mapping from yp to yn
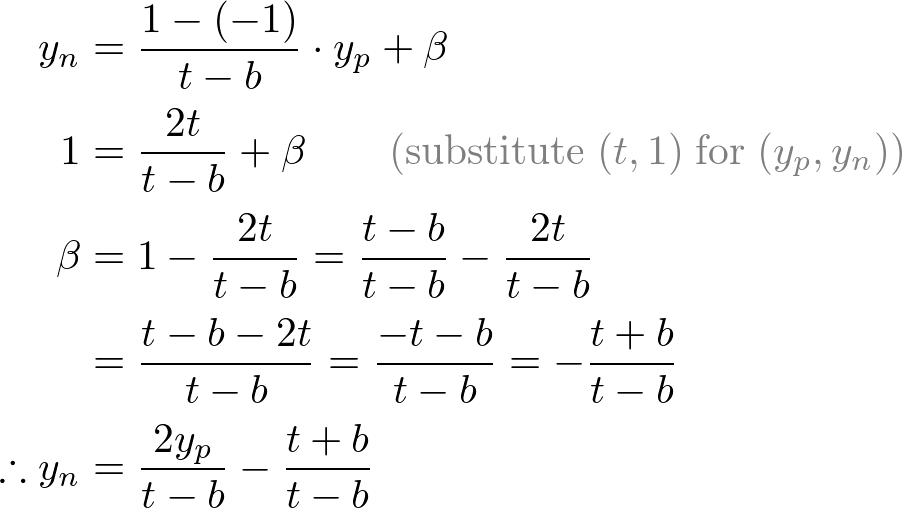
Then, we substitute xp and yp into the above equations.
Note that we make both terms of each equation divisible by -ze for perspective division (xc /wc , yc /wc ). And we set wc to -ze earlier, and the terms inside parentheses become xc and yc of clip coordiantes.
From these equations, we can find the 1st and 2nd rows of GL_PROJECTION matrix.
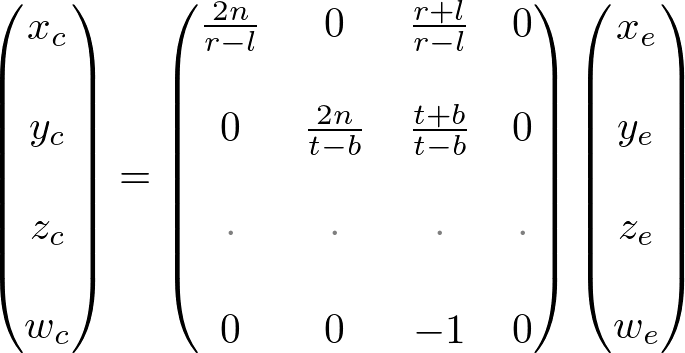
Now, we only have the 3rd row of GL_PROJECTION matrix to solve. Finding zn is a little different from others because ze in eye space is always projected to -n on the near plane. But we need unique z value for clipping and depth test. Plus, we should be able to unproject (inverse transform) it. Since we know z does not depend on x or y value, we borrow w-component to find the relationship between zn and ze . Therefore, we can specify the 3rd row of GL_PROJECTION matrix like this.
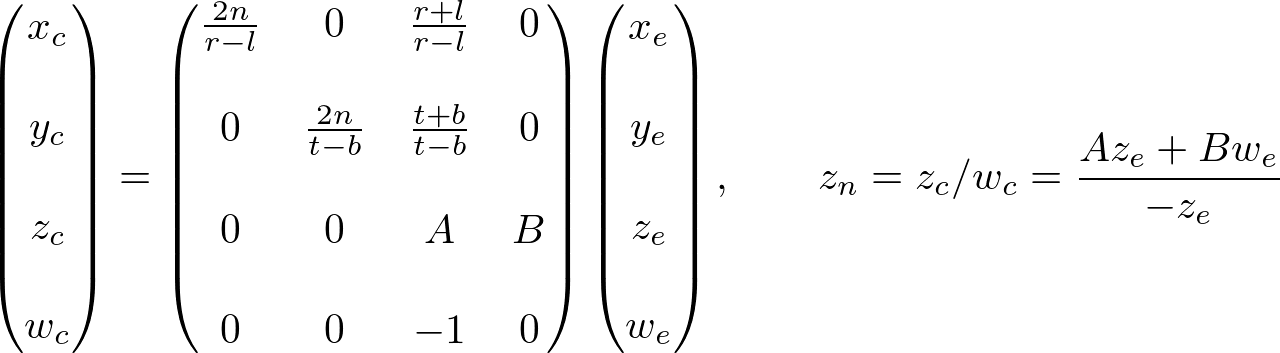
In eye space, we equals to 1. Therefore, the equation becomes;
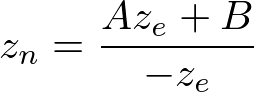
To find the coefficients, A and B , we use (ze , zn ) relation; (-n, -1) and (-f, 1), and put them into the above equation.
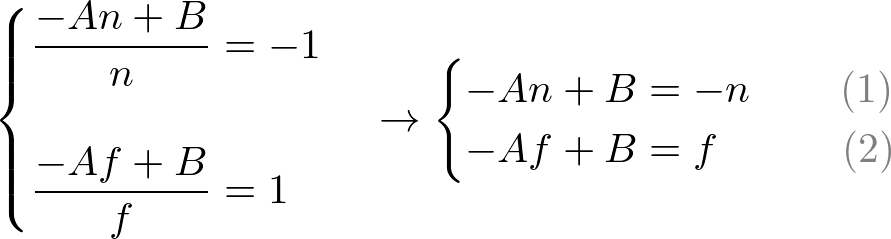
To solve the equations for A and B , rewrite eq.(1) for B;
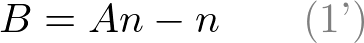
Substitute eq.(1') to B in eq.(2), then solve for A;
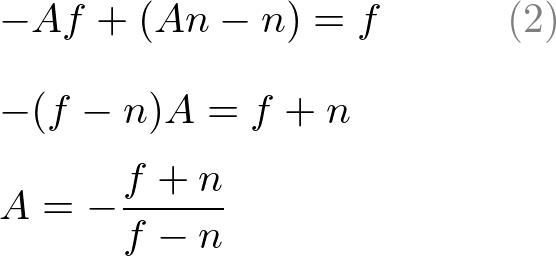
Put A into eq.(1) to find B ;
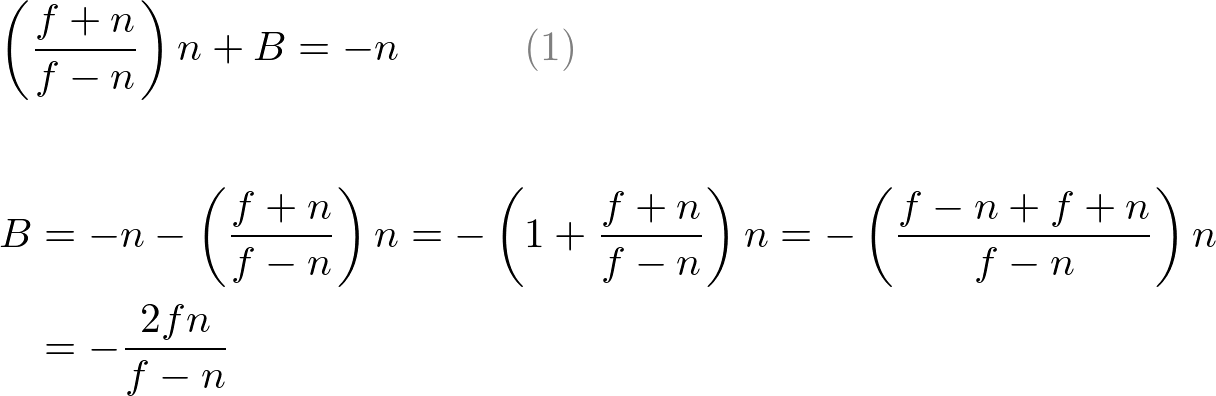
We found A and B . Therefore, the relation between ze and zn becomes;
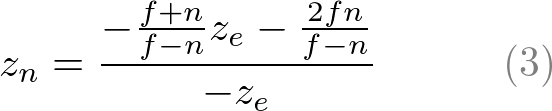
Finally, we found all entries of GL_PROJECTION matrix. The complete projection matrix is;
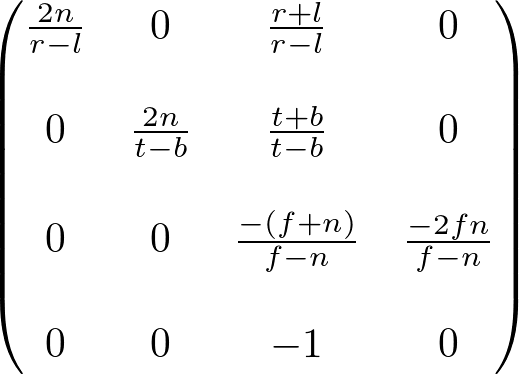
OpenGL Perspective Projection Matrix
This projection matrix is for general frustum. If the viewing volume is symmetric, which is 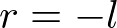 and
and 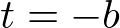 ,.then it can be simplified as;
,.then it can be simplified as;
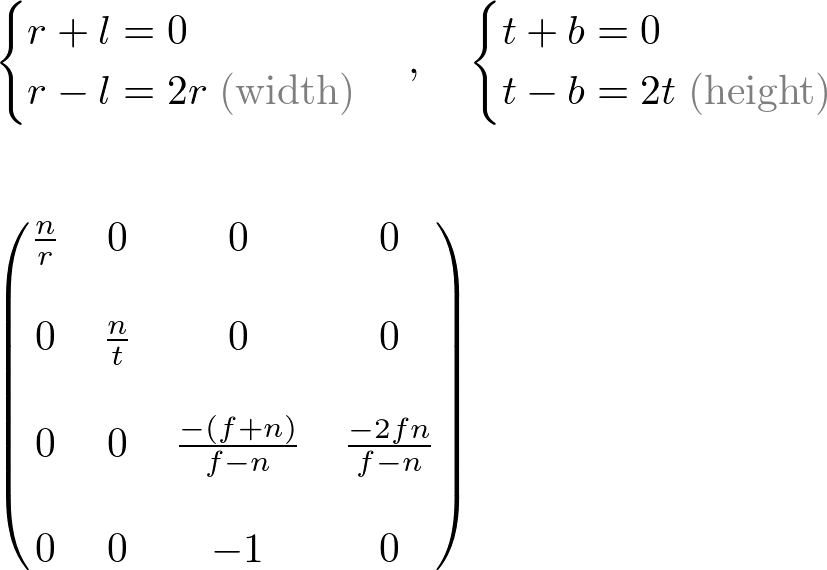
Before we move on, please take a look at the relation between ze and zn , eq.(3) once again. You notice it is a rational function and is non-linear relationship between ze and zn . It means there is very high precision at the near plane, but very little precision at the far plane. If the range [-n, -f] is getting larger, it causes a depth precision problem (z-fighting); a small change of ze around the far plane does not affect on zn value. The distance between n and f should be short as possible to minimize the depth buffer precision problem.
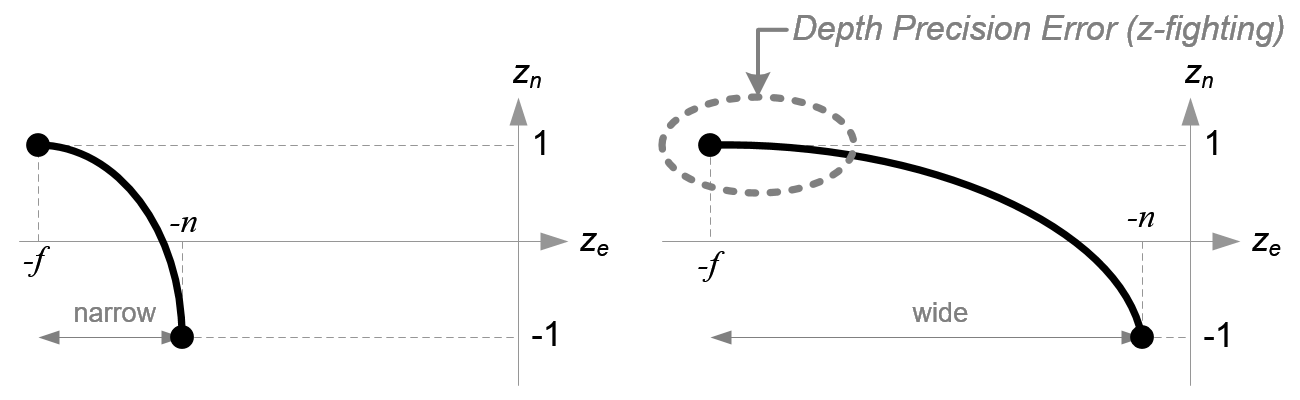 Comparison of Depth Buffer Precisions
Comparison of Depth Buffer Precisions
Orthographic Projection
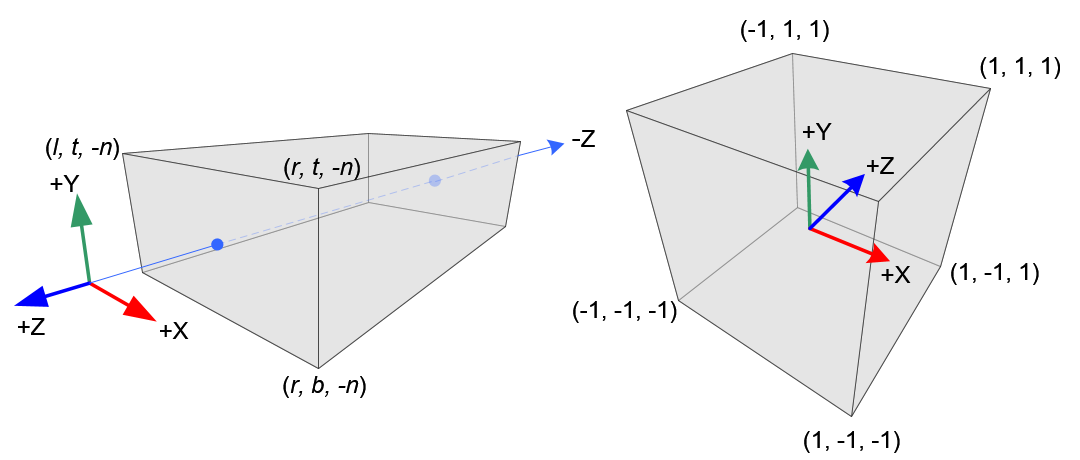 Orthographic Volume and Normalized Device Coordinates (NDC)
Orthographic Volume and Normalized Device Coordinates (NDC)
Constructing GL_PROJECTION matrix for orthographic projection is much simpler than perspective mode.
All xe , ye and ze components in eye space are linearly mapped to NDC. We just need to scale a rectangular volume to a cube, then move it to the origin. Let's find out the elements of GL_PROJECTION using linear relationship.
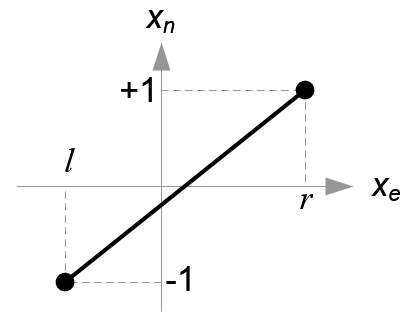 Mapping from xe to xn
Mapping from xe to xn
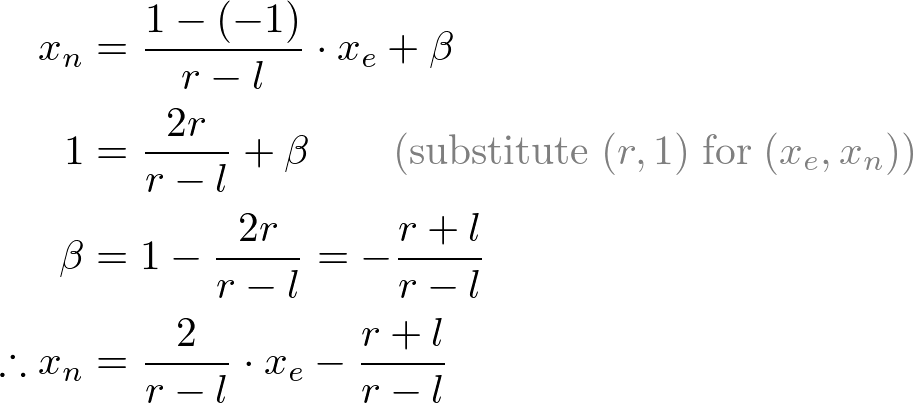
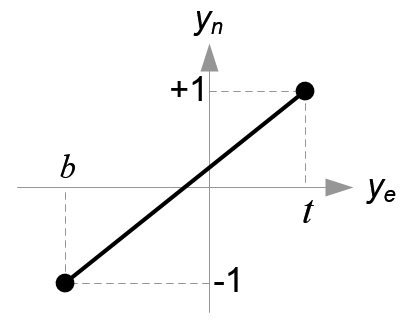 Mapping from ye to yn
Mapping from ye to yn
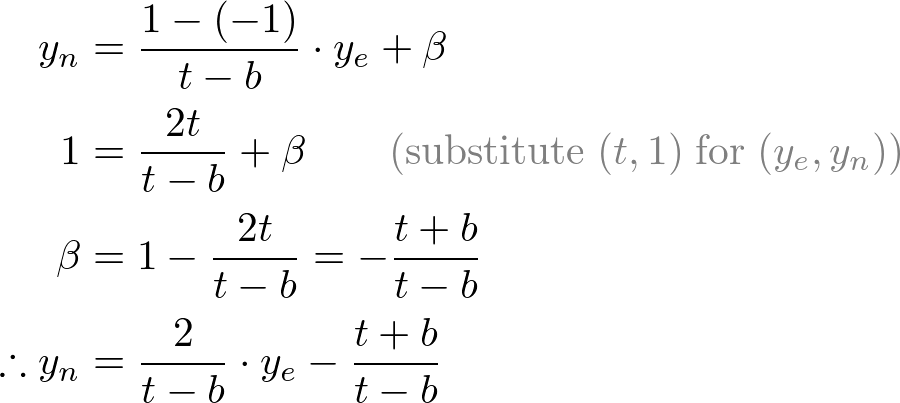
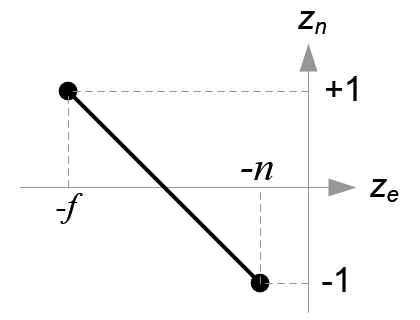 Mapping from ze to zn
Mapping from ze to zn
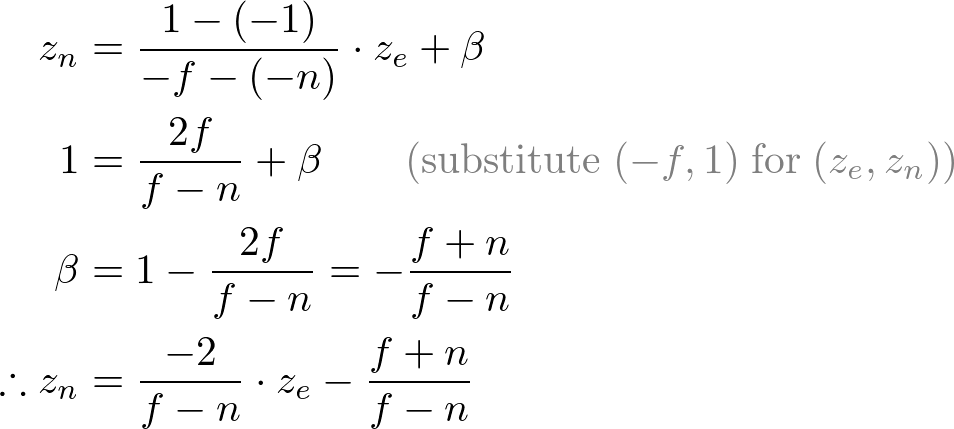
Since w-component is not necessary for orthographic projection, the 4th row of GL_PROJECTION matrix remains as (0, 0, 0, 1). Therefore, the complete GL_PROJECTION matrix for orthographic projection is;
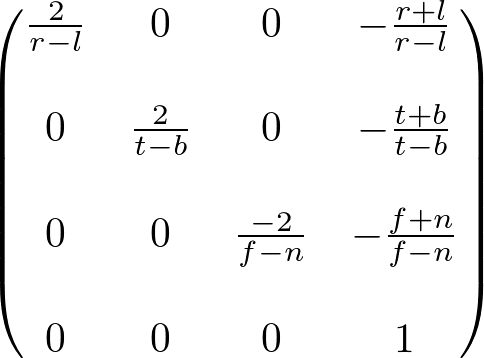
OpenGL Orthographic Projection Matrix
It can be further simplified if the viewing volume is symmetrical, 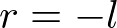 and
and 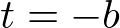 .
.
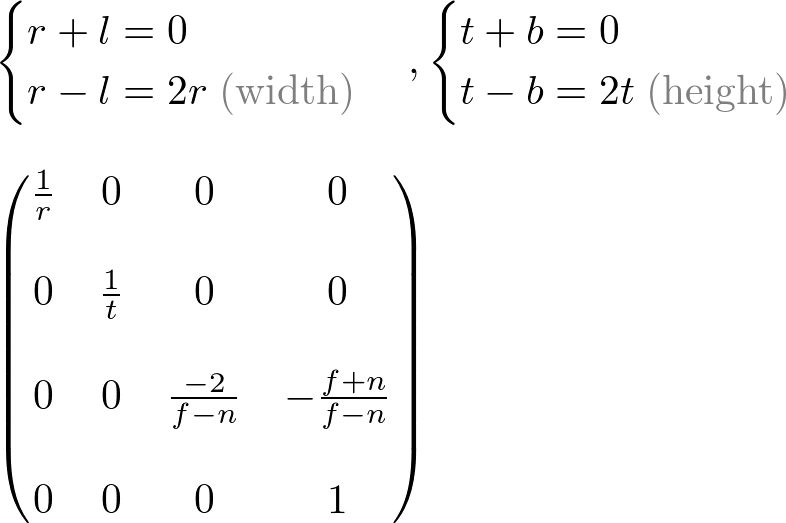
分享到:










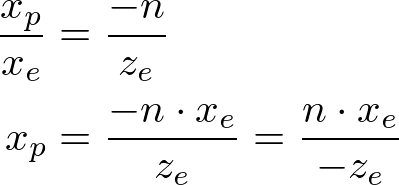
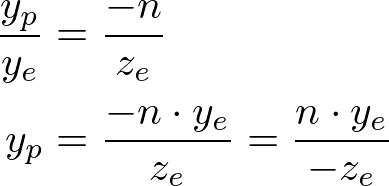

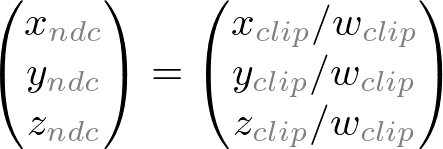
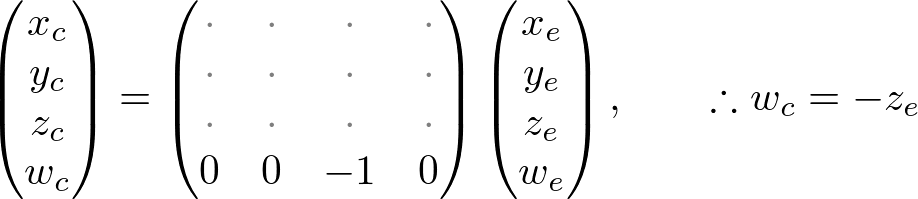

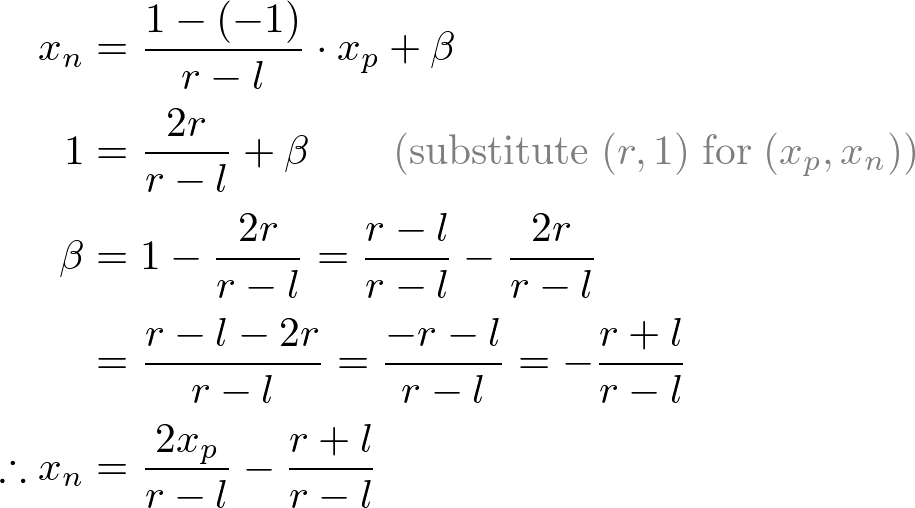

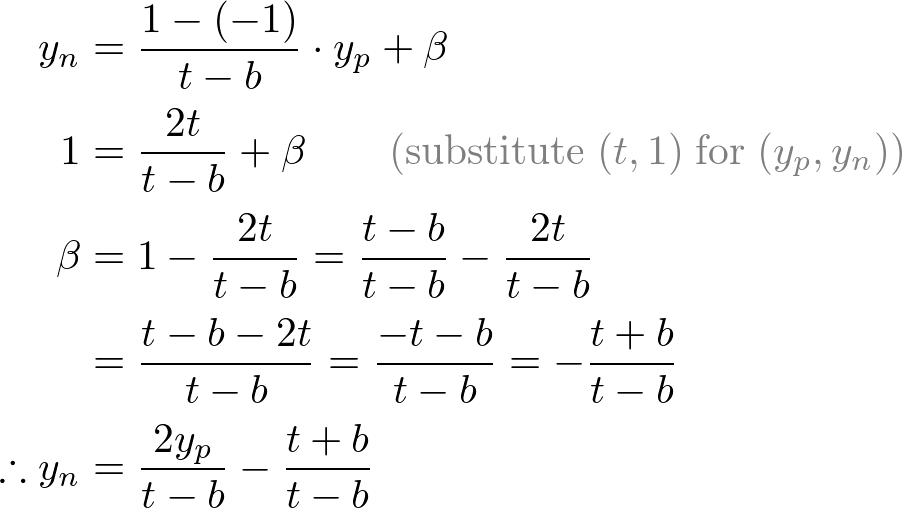
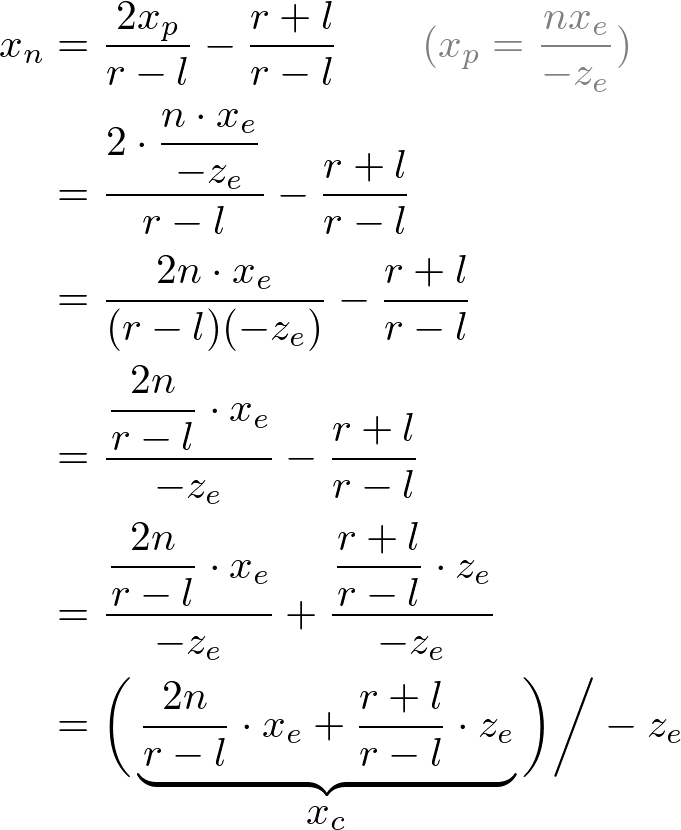
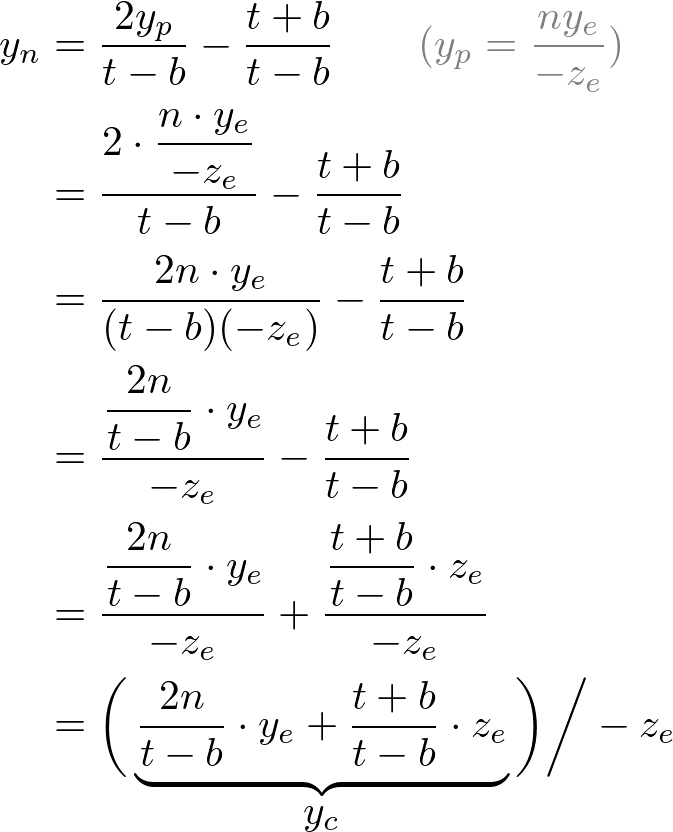
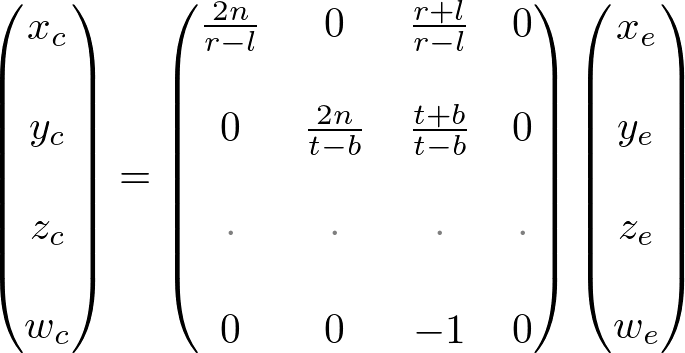
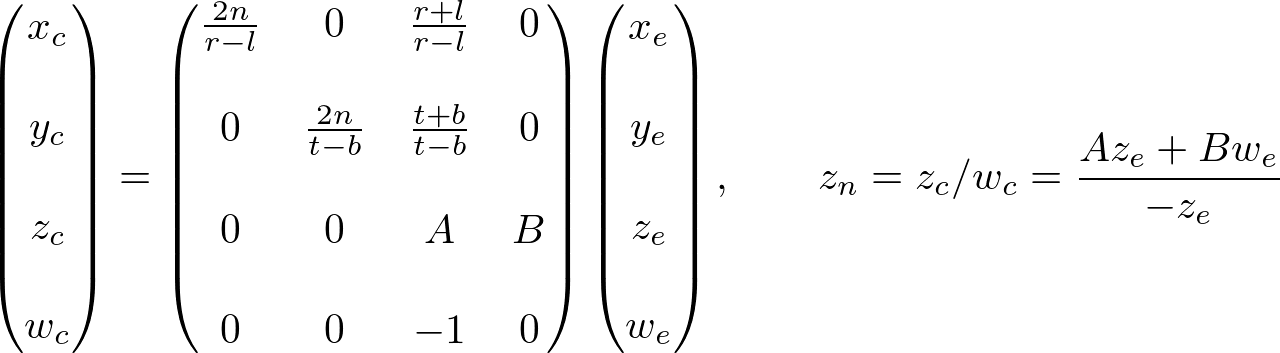
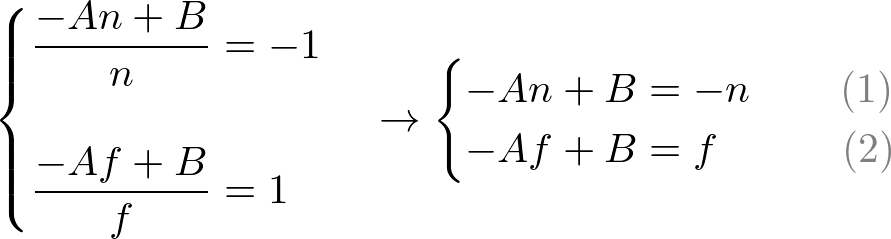
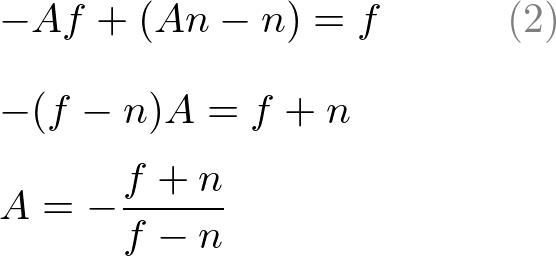
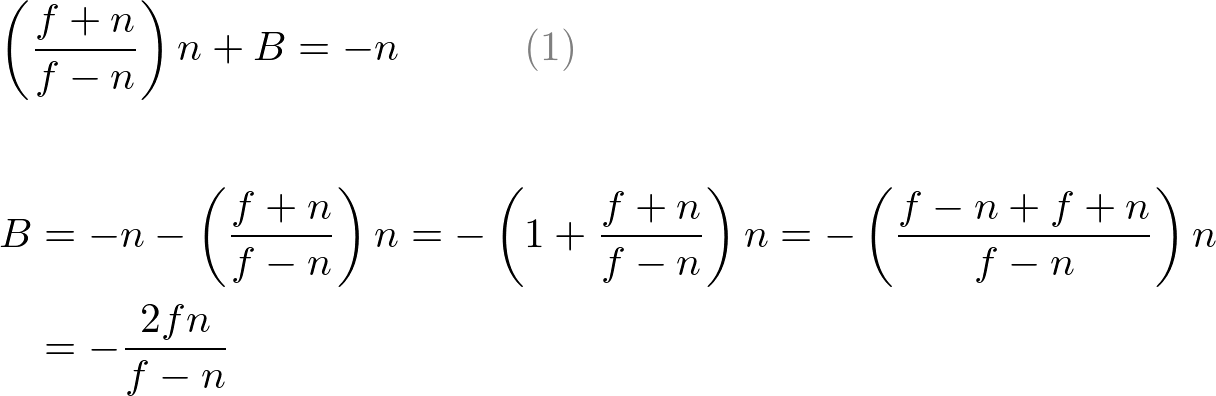
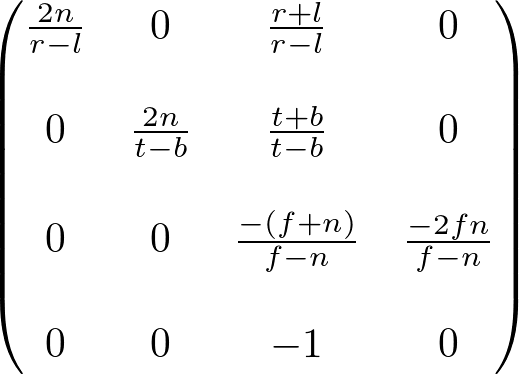
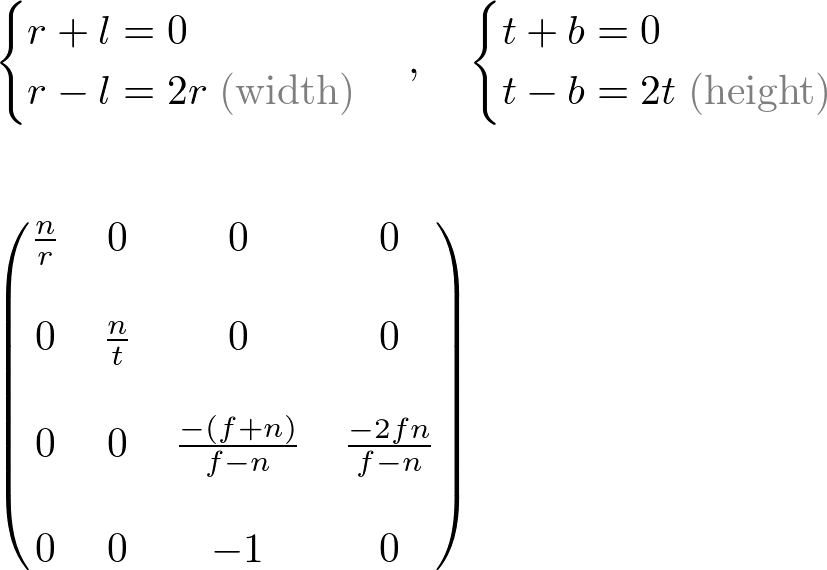



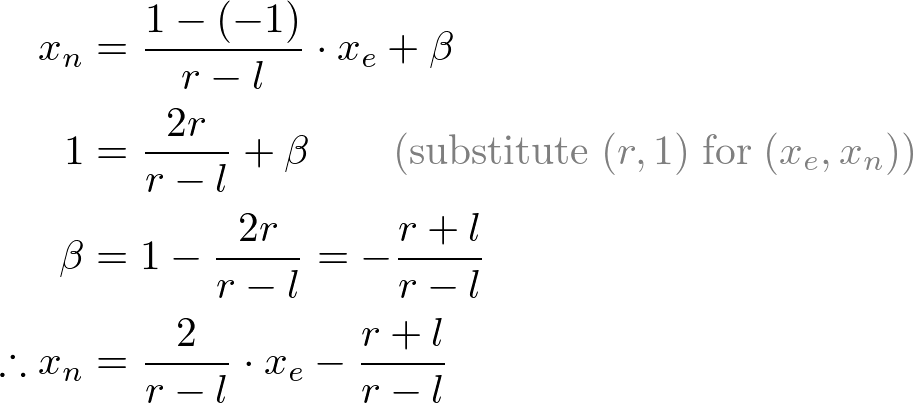

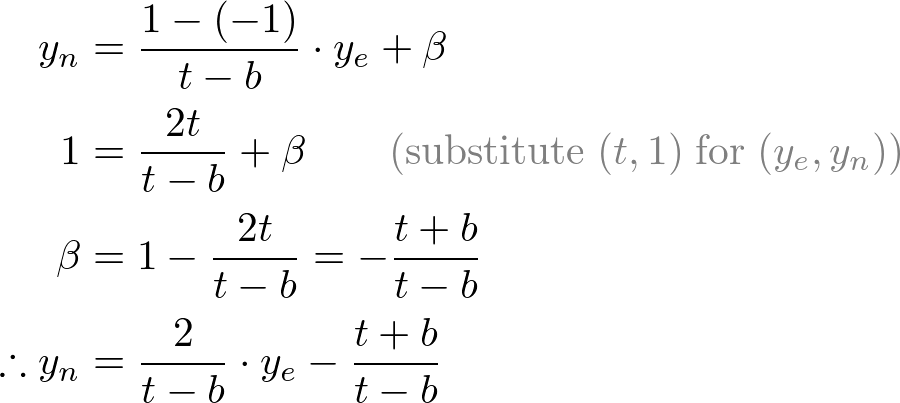

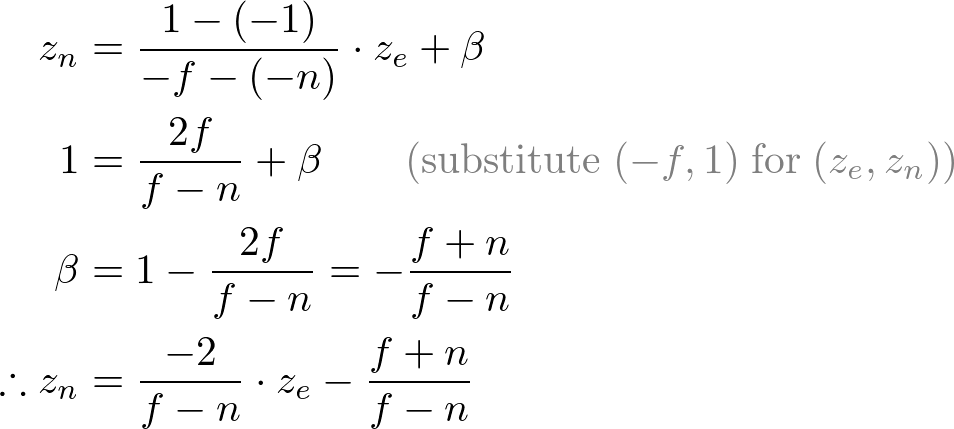
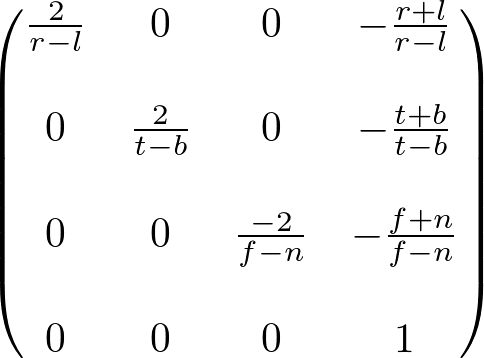
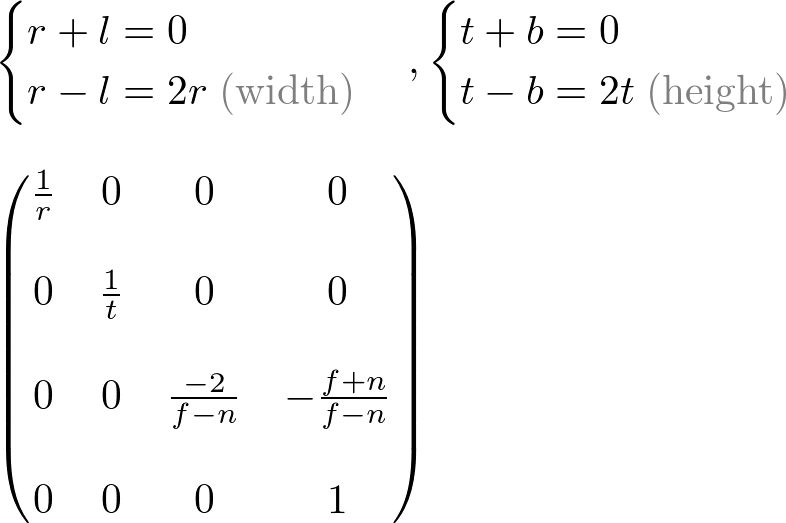



相关推荐
投影矩阵的内部结构和如何推导在Eric Lengyel撰写的“From Camera to Screen”中有详细的介绍。Lengyel在该领域是一位专家,他所著的关于3D图形编程的书籍和文章常常被专业人士参考。他的一些资源可以在***网站上...
这些变换包括了从物体空间(object space)到世界空间(world space)、再到视点空间(view space)以及最后的投影空间(projection space)等步骤。本文主要关注的是从世界空间到视点空间的变换,即通过视点矩阵(View ...
内容概要:本文详细介绍了一种基于STM32单片机的数控线性稳压电源设计方案。该电源采用220V市电输入,经过工频变压器降压、全桥整流及电容滤波,最终输出稳定的直流电压。设计中采用了线性稳压调整器方案,通过STM32单片机控制TLC5615数模转换器,实现了电压的数控调整。系统具备恒压恒流输出、过流保护、温度监测等功能,并配有LCD1602显示屏和声光报警装置。所有设计资料(源程序、原理图、PCB)均经过验证,具有较高的学习和设计参考价值。 适合人群:电子工程专业学生、嵌入式系统开发者、硬件工程师。 使用场景及目标:适用于实验室、工业自动化等领域,需要稳定电源供应的场合。目标是帮助读者理解和掌握基于STM32的数控线性稳压电源设计方法,提高电源系统的可靠性和安全性。 其他说明:文中提供的设计资料详尽完整,有助于读者深入理解每个环节的工作原理和技术细节。
LeddarTech客户案例研究.pdf
# 压缩文件中包含: 中文文档 jar包下载地址 Maven依赖 Gradle依赖 源代码下载地址 # 本文件关键字: jar中文文档.zip,java,jar包,Maven,第三方jar包,组件,开源组件,第三方组件,Gradle,中文API文档,手册,开发手册,使用手册,参考手册 # 使用方法: 解压最外层zip,再解压其中的zip包,双击 【index.html】 文件,即可用浏览器打开、进行查看。 # 特殊说明: ·本文档为人性化翻译,精心制作,请放心使用。 ·只翻译了该翻译的内容,如:注释、说明、描述、用法讲解 等; ·不该翻译的内容保持原样,如:类名、方法名、包名、类型、关键字、代码 等。 # 温馨提示: (1)为了防止解压后路径太长导致浏览器无法打开,推荐在解压时选择“解压到当前文件夹”(放心,自带文件夹,文件不会散落一地); (2)有时,一套Java组件会有多个jar,所以在下载前,请仔细阅读本篇描述,以确保这就是你需要的文件;
毕业论文-手机壁纸-整站商业源码.zip
毕业论文-二手跳蚤市场V5.4.1带微信支付、广告插件-整站商业源码.zip
毕业论文-体育新闻-整站商业源码.zip
# 压缩文件中包含: 中文文档 jar包下载地址 Maven依赖 Gradle依赖 源代码下载地址 # 本文件关键字: jar中文文档.zip,java,jar包,Maven,第三方jar包,组件,开源组件,第三方组件,Gradle,中文API文档,手册,开发手册,使用手册,参考手册 # 使用方法: 解压最外层zip,再解压其中的zip包,双击 【index.html】 文件,即可用浏览器打开、进行查看。 # 特殊说明: ·本文档为人性化翻译,精心制作,请放心使用。 ·只翻译了该翻译的内容,如:注释、说明、描述、用法讲解 等; ·不该翻译的内容保持原样,如:类名、方法名、包名、类型、关键字、代码 等。 # 温馨提示: (1)为了防止解压后路径太长导致浏览器无法打开,推荐在解压时选择“解压到当前文件夹”(放心,自带文件夹,文件不会散落一地); (2)有时,一套Java组件会有多个jar,所以在下载前,请仔细阅读本篇描述,以确保这就是你需要的文件;
傅里叶变换函数,Matlab脚本,可以直接调用
内容概要:本文档是2016年TI杯大学生电子设计竞赛G题——简易电子秤的设计要求与评分标准。任务要求设计并制作一个以电阻应变片为称重传感器的简易电子秤,其支架高度不超过40cm,悬臂梁上粘贴电阻应变片。具体要求包括:能以克为单位显示重量(10分),称重范围5.00g~500g且误差控制在特定范围内(50分),可设置单价并计算物品金额及累加(15分),具有去皮功能(15分),以及附加功能(10分)。设计报告涵盖方案论证、理论分析、电路与程序设计、测试方案及结果、报告结构及规范性(共20分)。此外,强调称重传感装置需自制,测试时以砝码为标准。 适合人群:电子工程及相关专业的学生或对电子设计有兴趣的学习者,尤其是准备参加类似竞赛的学生。 使用场景及目标:用于指导参赛选手完成竞赛作品,帮助他们理解竞赛的具体要求、评分细则,从而有针对性地进行设计与制作,确保作品符合竞赛规则。 其他说明:文档不仅提供了详细的任务要求,还明确了评分标准,有助于参赛者全面把握设计重点,合理分配时间和精力。同时,对于非参赛者而言,也是一个很好的学习案例,有助于了解电子秤的工作原理及设计思路。
灭火器识别数据集,识别率99.5%,分别率640x640,127张训练图,支持yolov7格式的标注框
# 压缩文件中包含: 中文-英文对照文档 jar包下载地址 Maven依赖 Gradle依赖 源代码下载地址 # 本文件关键字: jar中文-英文对照文档.zip,java,jar包,Maven,第三方jar包,组件,开源组件,第三方组件,Gradle,中文API文档,手册,开发手册,使用手册,参考手册 # 使用方法: 解压最外层zip,再解压其中的zip包,双击 【index.html】 文件,即可用浏览器打开、进行查看。 # 特殊说明: ·本文档为人性化翻译,精心制作,请放心使用。 ·只翻译了该翻译的内容,如:注释、说明、描述、用法讲解 等; ·不该翻译的内容保持原样,如:类名、方法名、包名、类型、关键字、代码 等。 # 温馨提示: (1)为了防止解压后路径太长导致浏览器无法打开,推荐在解压时选择“解压到当前文件夹”(放心,自带文件夹,文件不会散落一地); (2)有时,一套Java组件会有多个jar,所以在下载前,请仔细阅读本篇描述,以确保这就是你需要的文件;
内容概要:本文详细介绍了三相模块化多电平转换器(MMC)在开环控制环境下的运行机制和技术细节。首先,文章解释了MMC的基本概念,强调其高电压等级、模块化设计和灵活的拓扑结构。接着,阐述了开环控制策略,尤其是PWM脉冲发生器的作用,它根据预设的电压和电流参考值生成PWM信号,用于控制各子模块的通断状态。然后,描述了每个臂由四个功率模块组成的子模块与功率配置,确保电能的高效转换。再者,讨论了MMC与RLC结构或更大电网的连接方法,使其能够模拟不同负载条件并提供稳定电力输出。最后,介绍了示波器的应用,通过实时监测关键参数来评估和优化MMC的性能。 适合人群:从事电力电子领域的研究人员、工程师和技术爱好者。 使用场景及目标:适用于希望深入了解MMC工作原理及其在实际电力系统中应用的专业人士。目标是掌握MMC的设计、控制和优化方法,提高电力转换效率和稳定性。 其他说明:本文提供了丰富的理论背景和技术细节,对于理解和应用MMC技术具有重要指导意义。
基于python+NSGA2算法的供水管网水质监测点布局+源码+项目文档,适合毕业设计、课程设计、项目开发。项目源码已经过严格测试,可以放心参考并在此基础上延申使用,详情见md文档 供水管网水质监测点/传感器布局优化 1.基于整数编码的NSGA2算法 2.最短监测时间与最大监测概率双目标函数 3.使用基于epanet的wntr库进行水力水质模拟,并处理结果 4.将处理结果代入NSGA2算法, 迭代计算出结果 5. 所有功能基本实现, 流程基本可以走通 程序概述 本程序主要是解决供水管网水质监测点的布局优化问题; 面向的是突发污染情况下的水质监测点选取,因此需要多节点进行水质污染注入实验; 之前的做法都是使用epanet的程序包,链接库,但USEPA之后开源了基于Python的水力水质模拟库WNTR; 因此本程序使用了WNTR进行水力水质模拟,编写了水质模拟、数据处理模块;用于解决污染实验的实现与数据收集处理; 由于选择监测点是布局优化问题,因此使用了常见的进化算法NSGA2——非支配遗传算法; 水质监测布局常用的目标是最小化监测时间和最大化监测事件,即一组监测点尽可能对污染事件发生响应最快,对污染事件监测到的数量最多即为最优,但两个目标属于负相关。 有关帕累托解、NGSA2算法请自行搜索其他资料。 本程序实现了水质模拟、数据处理、算法迭代的全部过程。
内容概要:本文详细探讨了双馈风机(DFIG)低电压穿越(LVRT)能力的MATLAB仿真模型。首先介绍了转子侧变换器的控制策略,采用了基于定子电压定向的矢量控制方法,实现了有功无功解耦,并具备最大功率跟踪(MPPT)能力。其次,网侧变换器则采用电网电压定向的矢量控制策略,确保直流母线电压稳定,输入功率因数为1。此外,还深入解析了Crowbar电路的设计及其保护机制,当直流母线电压或转子电流超出设定阈值时,Crowbar电路将启动,防止系统损坏。仿真模型分为三层架构:风速模型和机械传动链、双PWM变流器控制层、电网故障模拟模块。最终通过仿真验证了系统的稳定性和有效性。 适合人群:从事风电系统设计、电力电子控制、MATLAB仿真等相关领域的工程师和技术人员。 使用场景及目标:适用于需要理解和优化双馈风机低电压穿越特性的研究人员和工程师。主要目标是掌握DFIG的LVRT控制策略,特别是矢量控制和Crowbar电路的工作原理,从而提高系统的可靠性和稳定性。 其他说明:文中提供了具体的MATLAB代码片段,帮助读者更好地理解各个控制环节的具体实现。调试过程中需要注意PI参数的设置和各控制环之间的参数匹配,以确保系统的最佳性能。
汽车轮胎识别数据集,837张训练图 识别率99.5%,支持yolov5格式的标注
内容概要:本文详细介绍了脉振方波HFI(高频注入模型)的技术背景及其在TI283x系列处理器上的实现方法。首先阐述了脉振方波HFI的基本概念和技术优势,接着展示了如何用C语言编写模型代码来生成和调制脉振方波信号。随后,利用Matlab进行了详细的仿真实验,包括创建仿真环境、定义参数、生成信号、配置仿真逻辑以及最终的数据分析。通过这一系列操作,不仅加深了对脉振方波HFI的理解,还验证了模型的有效性和可行性。 适合人群:从事高频信号处理、嵌入式系统开发的研究人员和技术爱好者,尤其是那些希望深入了解脉振方波HFI机制的人士。 使用场景及目标:适用于需要研究或开发高频注入技术的实际项目中,帮助开发者掌握从理论到实践的具体流程,提高技术水平。 其他说明:文中提供的代码片段和仿真步骤均经过测试,确保能够正常运行并得到预期效果。同时,附带的相关文档也为进一步学习提供了丰富的参考资料。
毕业论文-8导航-整站商业源码.zip
数字电视条件接收系统简介,系统阐述各个组成部分内容