斯特灵公式是一条用来取n阶乘近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特灵公式十分好用,而且,即使在
n很小的时候,斯特灵公式的取值已经十分准确。
公式为: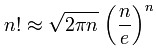
以下等式或者不等式均可以用数学归纳法予以证明!
1 + 3 + 5 + ... + (2n - 1) = n^2
1*2 + 2*3 + 3*4 + ... + n*(n + 1) = n*(n + 1)*(n + 2) / 3
1*1! + 2*2! + 3*3! + ... + n*n! = (n + 1)! - 1
1^2 + 2^2 + 3^2 + ... + n^2 = n*(n + 1)*(2n + 1) / 6
1^2 - 2^2 + 3^2 -... + (-1)^n * n^2 = (-1)^(n + 1) * n * (n + 1) / 2
2^2 + 4^2 + ... + (2n)^2 = 2n*(n+1)*(2n+1) / 3
1/2! + 2/3! + ... + n/(n+1)! = 1 - 1/(n+1)!
2^(n + 1) < 1 + (n + 1)2^n
1^3 + 2^3 + 3^3 + ... + n^3 = (n*(n + 1) / 2)^2
1/2n <= 1*3*5*...*(2n-1) / (2*4*6*...*2n) <= 1 / sqrt(n+1)<wbr>n=1,2...</wbr>
2^n >= n^2 , n=4, 5,...
2^n >= 2n + 1, n=3,4,...
r^0 + r^1 + ... + r^n < 1 / (1 - r), n>=0, 0<r<1
1*r^1 + 2*r^2 + ... + n*r^n < r / (1-r)^2, n>=1, 0<r<1
1/2^1 + 2/2^2 + 3/2^3 + ... + n /2^n < 2, n>=1
<wbr></wbr>
5^n - 1能被4整除
7^n - 1能被6整除
11^n - 6能被5整除
6*7^n - 2*3^n能被4整除
3^n + 7^n - 2能被8整除
<wbr></wbr>
n条直线能将平面最多划分为(n^2 + n + 2) / 2个区域
定义H(k) = 1 + 1/2 + 1/3 + ... + 1/k 则 1 + n/2 <=H(2^n) <= 1 + n
H(1) + H(2) + ... + H(n) = (n + 1) * H(n) - n
1*H(1) + 2*H(2) + ... + n*H(n) = n*(n + 1) / 2 * H(n + 1) - n * (n + 1) / 4
欧拉函数的定义:E(k)=([1,n-1]中与n互质的整数个数).因为任意正整数都可以唯一表示成如下形式:
k=p1^a1*p2^a2*……*pi^ai;(即分解质因数形式)
可以推出:E(k)=(p1-1)(p2-1)……(pi-1)*(p1^(a1-1))(p2^(a2-1))……(pi^(ai-1))
<wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>=k*(p1-1)(p2-1)……(pi-1)/(p1*p2*……pi);<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>=k*(1-1/p1)*(1-1/p2)....(1-1/pk)</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
在程序中利用欧拉函数如下性质,可以快速求出欧拉函数的值(a为N的质因素)
若(N%a==0 && (N/a)%a==0) 则有:E(N)=E(N/a)*a;
若(N%a==0 && (N/a)%a!=0) 则有:E(N)=E(N/a)*(a-1);
若N>2, 欧拉函数E(N)必定是偶数
若gcd(a,b) = 1,则有E(a * b) = E(a) * E(b)
若一个数N分解成p1^a1 * p2^a2 * ... * pn^an,那么
E(N) = p1^(a1 - 1) * (p1 - 1) * ... * pn^(an - 1) * (pn - 1)
若N>1,不大于N且与N互素的所有正整数的和是1/2 * N * E(N)
因子和: 若 k=p1^a1*p2^a2...*pi^ai<wbr><wbr>F(k) = (p1^0+...+p1^a1)*(p2^0+...+p2^a2)*...*(pi^0 + ... + pi^ai)<br><wbr></wbr></wbr></wbr>
没有一个平方数是以2,3,7,8结尾的
max{a, b, c} - min{a, b, c} = (|a - b| + |b - c| + |a - c|) / 2
ac % m = bc % m 可以得到 a % m' = b % m'<wbr>m' = m / gcd(m, c)</wbr>
如果a % mi = b % mi (i=1,2,...,n) 并且 l = lcm(m1, m2, ..., mn)<wbr>则可以得到 a % l = b % l</wbr>
Euler 定理
若gcd(a,m)==1, 则a^(phi(m)) % m = 1 % m
Fermat小定理
p为素数,对任意的a有 a^p % p = a % p
p为素数 ,对任意的a(a<p), a^(p-1) % p = 1 % p
p为素数 , 对任意的a,若gcd(p,a)==1, a^(p-1) % p = 1 % p
一个奇数a的平方减1都是8的倍数
任意4个连续整数的乘积再加上1 一定是完全平方数
当a是整数时,a(a-1)(2a-1)是6的倍数
当a是奇数时,<wbr><wbr>a(a^2 - 1)是24的倍数</wbr></wbr>
n次代数方程 x^n + a1 * x^(n-1) + ... + an-1*x + an = 0 的系数都是a1, a2, ... , an都是整数。
如果它有有理数的根,证明这个根一定是整数,而且这个数一定是an的因子。如果不是整数,就一定是无理数。
设a,b都是正整数,a<b而gcd(a,b) = 1 ,如果存在一个素数p,它能够整除b,但是不能够整除10,则a/b一定不能够化成有限小数。如果b=2^a * 5^b,其中a,b都是非负整数,则a/b能化成有限小数。
设0<a<b, 且gcd(a,b) = 1, 如果a/b能表示成纯循环小数,则我们有gcd(b, 10) = 1。
设0<a<b, 且gcd(a,b) = 1, 令h是一个最小的正整数,使得10^h 与1 关于b同余,那么a/b可以表示成纯循环小数
0.d1d2d3...dh。
设b是一个正整数且gcd(10, b) = 1,令h是一个最小的正整数,能使得10^h 与1 关于b同余,则h能够整除Euler(b)
设a, b, b1都是正整数,a < b, gcd(a, b) = 1, b1 > 1, gcd(b1, 10) = 1。b = 2^c * 5^d * b1, 其中c, d都是非负整数,且不同时为0, 令h是一个最小的正整数,使得 10^h 与1 关于b1同余, 则当c>=d时,我们有a/b = 0.a1a2...aca'(c+1)...a'(c + h)<wbr>,而当c <
d时,我们有a/b = 0.a1a2...ada'(d+1)...a'(d + h)</wbr>
设0.a1a2...an...不能换成有限小数,也不能化成循环小数,则它不能化成分数。
设p是一个素数,m是一个正整数且m=na+b其中a是一个非负整数而b是一个不大于n-1的非负整数。令
a=p^m, 当b=0的时候,a的开n次方是一个整数,当1<= b <= n - 1时,a的开n次方不能表示为分数。
设p是一个素数,m是一个正整数且m=na+b其中a是一个非负整数而b是一个不大于n-1的非负整数。令
a=p^m, 当b=0的时候,a的开n次方是一个整数,当1<= b <= n - 1时,a的开n次方=b+c, 其中b是一个正整数而c是一个无限小数但不是循环小数。
设a是一个正整数, 当a的开n次方=b+c中b是一个正整数而0<c<1时,则a的开n次方不能表示成为分数,并且这时c是一个无限小数但不是循环小数。
(4b^3 + 3b) / (4b^2 + 1) <= b + 1 / (2b + 1/2b) <=<wbr>根号b平方+1 <= b + 1 / (2b + 1/(2b + 1 / 2b)) = (8b^4 + 8b^2 + 1) / (8b^3 + 4b)</wbr>
b + 1/(2b + 1/(2b + 1/(2b + 1/2b))) <= 根号b平方+1
(16b^5 + 20b^3 + 5b) / (16b^4 + 12b^2 + 1) <= 根号b平方+1 <= (8b^4 + 8b^2 + 1) / (8b^3 + 4b)
<wbr></wbr>
8*8棋盘2牌的完美覆盖数目为12988816=2^4 * 901^2
<wbr></wbr>
一张m行n列棋盘有一个b-牌的完美覆盖,当且仅当b是m的一个因子或者b是n的一个因子
<wbr></wbr>
n阶幻方的幻和为 n*(n^2+1) / 2<wbr><wbr>n阶幻方体的幻和为(n^4+n) / 2</wbr></wbr>
<wbr></wbr>
鸽巢原理: 如果n+1个物体被放进n个盒子,那么至少有一个盒子包含两个或者更多的物体
鸽巢原理加强形式: 令q1,q2,..,qn为正整数。如果将 q1+q2+...+qn-n+1 个物体放入n个盒子内,那么,至少第一个盒子至少含有q1个物体,或者第二个
盒子至少含有q2个物体,... ,或者第n个盒子至少含有qn个物体
<wbr></wbr>
给定m个整数a1,a2,...,am,存在整数p和q,0<=p<q<=m,使得a(p+1)+a(p+2)+...+a(m)能够被m整除。通俗的说,就是在序列a1,a2,...,am中存在连续
个a,使得这些a的和能被m整除
<wbr></wbr>
由n^2+1个实数构成的序列a1,a2,...,a(n^2+1)或者含有长度为n+1的递增子序列,或者含有长度为n+1的递减子序列
<wbr></wbr>
Ramsey定理:在6个(或更多的)人中,或者有3个人,他们中的每两个人都互相认识;或者有3个人,他们中的每两个人都彼此不认识
<wbr></wbr>
n个元素的集合的循环r-排列的个数由
A(n,r)/r=n!/(r * (n-r)!)给出。特别地,n个元素的循环排列的个数是(n-1)!
<wbr></wbr>
多重集排列:
令S是一个多重集,有k个不同类型的元素,各元素的重数分别为n1,n2,...,nk。设S的大小为n=n1+n2+...+nk。则S的排列数等于n!/(n1!*n2!*...*nk!)
<wbr></wbr>
多重集的组合:
令S为具有k中类型元素的一个多重集,每种元素均具有无限的重复数。则S的r-组合的个数等于 C(r+k-1,r)
<wbr></wbr>
如果排列P1P2...Pn有逆序列b1,b2,...,bn,且k=b1+b2+...+bn为逆序数,那么P1P2...Pn可以通过k次连续交换得到12...n
<wbr></wbr>
利用反射Gray码生成相邻元组1的个数相差1的所有组合
<wbr></wbr>
生成{1,2,...,n}的字典序r-组合的算法:
从r-组合a1a2...ar=12..r开始
当a1a2...ar不等于(n-r+1)(n-r+2)...n时,做:
i)确定最大的整数k,是的ak + 1<=n且ak + 1不等于a1,a2,...ar
ii)用r-组合<wbr><wbr>a1...a(k-1)(ak + 1)(ak+2)...(ak + r - k + 1)替换 a1a2...ar</wbr></wbr>
<wbr></wbr>
C(n,k)=C(n-1,k)+C(n-1,k-1)<wbr>1<=k<=n-1</wbr>
<wbr></wbr>
k * C(n,k) = n * C(n-1, k-1)
<wbr></wbr>
C(n,0)+C(n,1)+...+C(n,n) = 2^n<wbr><wbr><wbr>C(n,0)+C(n,2)+... = 2^(n-1)<wbr>C(n,1)+C(n,3)+...=2^(n-1)</wbr></wbr></wbr></wbr>
<wbr></wbr>
1*C(n,1)+2*C(n,2)+...+n*C(n,n)=n*2^(n-1) (n>=1)
<wbr></wbr>
通过对等式 (1+x)^n=sigma(C(n,k)*x^k)<wbr>k: 0->n 两边就微分,可以得到 sigma(k^p * C(n,k)) k: 1->n的和</wbr>
<wbr></wbr>
sigma(C(n,k)^2) = C(2n,n)<wbr>k:<wbr>1->n</wbr></wbr>
<wbr></wbr>
C(r,0)+C(r+1,1)+...+C(r+k,k) = C(r+k+1,k)
<wbr></wbr>
C(0,k)+C(1,k)+...+C(n-1,k)+C(n,k)=C(n+1,k+1)
<wbr></wbr>
Dilworth定理:<wbr>令(X,<=)是一个有限偏序集,并令m是反链的最大大小。则X可以被划分成m个但不能再少的链</wbr>
同理, 若r是链的最大大小,那么X可以被划分成r个但不能再少的反链。
<wbr></wbr>
卷积定理: 对任意两个长度为n的向量a和b,其中n是2的幂,
a,b的卷积等于 (DFT2n)-1(DFT2n(a) . DFT2n(b))
其中向量a和b是用0扩充使其长度达到2n,"."表示2个2n个元素组成的向量的点乘
<wbr></wbr>
18014398509481931 素数
18014398509482111 最小质因子为11
1637672591771101 最小质因子为6780253
<wbr></wbr>
中线定理(pappus定理)是指三角形ABC内BM=MC,则AB^2+AC^2=2*(AM^2+BM^2)
证明:
AC^2=AH^2+HC^2?
AB^2=AH^2+BH^2=AH^2+(HC+2MH)^2=AH^2+HC^2+4MH*HC+4MH^2
左边=AB^2+AC^2=2*AH^2+2CH^2+4MH*CH+4MH^2
右边=2*(AM^2+BM^2)=2*(AH^2+MH^2+(CH+MH)^2)=2*(AH^2+MH^2+CH^2+2CH*MH+MH^2)
得证
<wbr></wbr>
[modified from &豪's blog]
(1)定理:设x0,x1,x2,...是无穷实数列,xj>0,j>=1,那么,
<wbr><wbr><wbr><wbr><wbr>(i)对任意的整数 n>= 1, r>=1有<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><X0,...,Xn-1,Xn,...,Xn+r> = <X0,...,Xn-1,<Xn,...,Xn+r>><br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>=<wbr><wbr><X0,...,Xn-1,Xn+1/<Xn+1,...,Xn+r>>.<br><wbr><wbr><wbr><wbr><wbr>特别地有<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><X0,...,Xn-1,Xn,Xn+1> = <X0,...,Xn-1,Xn+1/Xn+1><br><wbr><wbr><wbr><wbr><wbr>注:用该定理可以求连分数的值</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
(2)对于连分数数数列 <X0,...Xn> 有递推关系:
<wbr><wbr><wbr><wbr><wbr>Pn = XnPn-1+Pn-2;<br><wbr><wbr><wbr><wbr><wbr>Qn = XnQn-1+Qn-2;<br><wbr><wbr><wbr><wbr><wbr>定义:<wbr>P-2 = 0; P-1 = 1; Q-2 = 1; Q-1 = 0;<br><wbr><wbr><wbr><wbr><wbr>所以:<wbr>P0 = X0; Q0 = 1; P1 = X1X0+1; Q1 = X1;<br><wbr><wbr><wbr><wbr><wbr>特别地:当 Xi=1 时, {Pn}, {Qn}为Fbi数列</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
(3)对于连分数数数列 <X0,...Xn>
<wbr><wbr><wbr><wbr>当n>= 1时,我们有PkQk-1 = Pk-1Qk = (-1)^k<br><wbr><wbr><wbr><wbr>当n>=2时, 我们有PkQk-2 = Pk-2Qk = (-1)^(k - 1) * xk</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
(4) 所有有理数都可以表示成有限连分数
(5)pell方程: x^2+ny^2=+-1的解法:
<wbr><wbr><wbr><wbr><wbr>若n是平方数,则无解, 否则:<br><wbr><wbr><wbr><wbr><wbr>先求出sqrt(n)的连分数序列<x0,x1..xn> 其中xn = 2*x0;<br><wbr><wbr><wbr><wbr><wbr>对于 x^2+ny^2=-1<br><wbr><wbr><wbr><wbr><wbr>若n为奇数,则 x=Pn-1, y=Qn-1; n为偶数时无解<br><wbr><wbr><wbr><wbr><wbr>对于 x^2+ny^2=1<br><wbr><wbr><wbr><wbr><wbr>若n为偶数,则 x=Pn-1, y=Qn-1; n为奇数时x=P2n-1, y=Q2n-1<br><wbr><wbr><wbr><wbr><wbr>注:以上说的解均为最小正解</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
分享到:










相关推荐
我09年参加现场赛前准备的,这些公式有的是在POJ等OJ上做题时遇到的,还有些可能会出现的数学公式,本人非数学出身,准备的内容尚浅,就是多和乱(不敢说丰富)
编程,搞ACM必备的数论公式 ,超有用 ,
数论是Acm中的重点内容。历年竞赛题目, 一般都有1-2道与数论有密切关系。数论涉及的概念 和算法很多,用途也非常广泛。掌握与数论有关的 方法,是参赛者需要具备的必要技能。
数论资源,里面又很多公式 数论资源,里面又很多公式 数论资源,里面又很多公式 数论资源,里面又很多公式
以下等式或者不等式均可以用数学归纳法予以证明! 1 + 3 + 5 + ... + (2n - 1) = n^2 1*2 + 2*3 + 3*4 + ... + n*(n + 1) = n*(n + 1)*(n + 2) / 3 1*1! + 2*2! + 3*3! + ......1^2 + 2^2 + 3^2 + ......
数论函数的性质研究在数论中占有举足轻重的地位,很多函数的单个取值是没有规律的,但是其均值往往具有非常规则的渐近公式。美籍罗马尼亚著名数论专家F.Smarandache教授引入了简单数的概念。如果正整数n的所有真因子的...
gcd和lcm相关公式衍生 4 三-素数问题 6 素数性质 6 素数猜想 6 素数测试 6 筛素数 7 区间筛素数 7 大素数测试 7 素因子相关 8 梅森素数 8 筛可以表示成x^2+(x+1)^2的素数 9 高斯整数环与高斯素数 10 n!中素数y的个数...
第二篇介绍解析数论的一些基本理论与方法,包括关于黎曼ζ函数与狄氏L函数的一些基本理论及应用这些理论来研究自然数申中或一般算术级数中的素数分布的方法等;第三篇系统地论述了:角和方法,包括有理型三角和、素...
第二部分主要研究了Hurwitzzeta函数的部分和的积分渐进公式,推广了专著[SC]一些结果;研究了zeta函数和Riemannzeta函数洛朗系数的算术性质;研究了有理数域上一类zeta函数有关计算的伪问题,给出了Eisenstein公式的...
在乘法数论中,在素数分解期间,用素数覆盖正整数可能被视为是并行系统的结果,当且仅当素数倒数的乘积的欧拉公式为真时,并行系统才能正常运行。 给出了质数小于或等于任意界限的精确公式。 可以使用Wolfram的...
《数学·统计学系列:三角级数论》以现代的观点简明而完整地讲述傅里叶级数的基础理论,全书共分7章。第1章讲述预备性知识;第2,3章讲傅里叶级数的性质;第4章讲傅里叶级数的收敛性及其判别法;第5章、第6章讲...
引入了两个数论函数,并给出它们在简单数序列集合中的渐近公式。
第一章 有关数论的算法 1.1最大公约数与最小公倍数 1.2有关素数的算法 1.3方程ax+by=c的整数解及应用 1.4 求a^b mod n 第二章 高精度计算 2.1高精度加法 2.2高精度减法 2.3高精度乘法 2.4 高精度除法 练习 第三章 ...
欧拉公式求长期率的matlab代码数论Python 实现数论资料的Python模块集合。 Number-Theory-Python软件包当前包括: NumbThy.pdf:数论短期课程 numbthy.py:基本数论函数 gaussint.py:对高斯整数的基本运算 ...
定义了整数标准分解式的数论函数β...标准分解式方法和解析数论的和均值方法,研究了函数β(n,p)及其均值的计算问题,给出整数n的标准分解式中的指数函数β(n,p)的计算公式,以及其均值∑βk(n,p)(k=1,2)的精确计算公式。
欧拉函数是数论中很重要的一个函数,欧拉函数是指:对于一个正整数 n ,小于 n 且和 n 互质的正整数(包括 1)的个数,记作 φ(n) 。 完全余数集合: 定义小于 n 且和 n 互质的数构成的集合为 Zn ,称呼这个集合为...
以及点集偏差和离差在拟Monte Carlo方法中的一些应用,如具有数论网点的多维求积公式的构造、多维数值积分的格法则、函数最大值近似计算的数论方法等;还给出了近二十年来的一些新进展。《点集偏差引论》可供大学...
这些理论的状态数的渐近增长可以用一个 取决于z的Cardy公式的扩展。 我们证明,如一百年前哈迪和拉曼努詹所提出的,通过将整数的分区计数为第z次幂可以恢复该结果。 这在色散关系的特征能量与圆柱半径和基态能量之间...
利用猜想、归纳,得出二进制数字之和函数九次均值的计算公式。
数论\ 阶乘最后非零位 模线性方程(组) 质数表 质数随机判定(miller_rabin) 质因数分解 最大公约数欧拉函数 数值计算\ 定积分计算(Romberg) 多项式求根(牛顿法) 周期性方程(追赶法) 图论_NP搜索\ 最大团(n...