摘取自维基百科:
http://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E5%BD%92%E7%BA%B3%E6%B3%95
数学归纳法(Mathematical Induction,通常简称为MI)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。虽然数学归纳法名字中有“归纳”,但是数学归纳法并不是不严谨的归纳推理法,它是属于完全严谨的演绎推理法。
定义
最简单和常见的数学归纳法是证明当 n 等于任意一个自然数时某命题成立。证明分下面两步:
- 证明当 n = 1 时命题成立。
- 证明如果在 n = m 时命题成立,那么可以推导出在 n = m+1 时命题也成立。(m 代表任意自然数)
这种方法的原理在于:首先证明在某个起点值时命题成立,然后证明从一个值到下一个值的过程有效。当这两点都已经证明,那么任意值都可以通过反复使用这个方法推导出来。把这个方法想成多米诺效应也许更容易理解一些。例如:你有一列很长的直立着的多米诺骨牌,如果你可以:
- 证明第一张骨牌会倒。
- 证明只要任意一张骨牌倒了,那么与其相邻的下一张骨牌也会倒。
那么便可以下结论:所有的骨牌都会倒。
例子
假设我们要证明下面这个公式(命题):

其中 n 为任意自然数。这是用于计算前 n 个自然数的和的简单公式。证明这个公式成立的步骤如下。
第一步
第一步是验证这个公式在 n = 1 时成立。我们有左边 = 1,而右边 = 1(1 + 1) / 2 = 1,所以这个公式在 n = 1 时成立。第一步完成。
第二步
我们先假设 n = m 时公式成立。即
 (等式 1)
(等式 1)
然后在等式等号两边分别加上 m + 1 得到
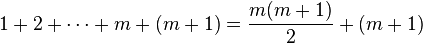 (等式 2)
(等式 2)
这就是 n = m+1 时的等式。我们现在需要根据等式 1 证明等式 2 成立。通过因式分解合并,等式 2 的右手边
![= \frac{m(m + 1)}{2} + \frac{2(m + 1)}{2}
= \frac{(m + 2)(m + 1)}{2}
= \frac{(m + 1)(m + 2)}{2}
= \frac{(m + 1)[(m + 1) + 1]}{2}.](http://upload.wikimedia.org/math/3/8/e/38eb7d58dad30505091f7aa911bc1c3d.png)
也就是说
![1 + 2 + \cdots + (m + 1) = \frac{(m + 1)[(m + 1) + 1]}{2}](http://upload.wikimedia.org/math/8/e/1/8e121ee42835ec53a1c0346c07d5d003.png)
这样便证明了从 P(m) 成立可以推导出 P(m+1) 也成立。证明至此结丛,结论:对于任意自然数 n,P(n) 均成立。
解释
在这个证明中,归纳推理的过程如下:
- 首先证明 P(1) 成立,即公式在 n = 1 时成立。
- 然后证明从 P(m) 成立可以推导出 P(m+1) 也成立。(这里实际应用的是演绎推理法)
- 根据上两条从 P(1) 成立可以推导出 P(1+1),也就是 P(2) 成立。
- 继续推导,可以知道 P(3)成立。
- 从 P(3) 成立可以推导出 P(4) 也成立。
- 不断重复推导下一命题成立的步骤。(这就是所谓“归纳”推理的地方)
- 我们便可以下结论:对于任意自然数 n,P(n) 成立。






相关推荐
重温基于图的协同过滤:一种线性残差图卷积网络方法,AAAI2020.zip
pythonxml:重温Python的XML工具pythonxml:重温Python的XML工具
但凡事大都有主要矛盾,学数学分析也应该抓主要思想。根据笔者这些年对 数学分析的体会,感觉有三大基本思想是数学分析的核心,逼近、变换和分解。 围绕微分、积分和级数这三大主题,展开上述三大基本思想,构成了...
因此,它涉及了除微积分以外的许多数学分支:主要有实和复分析、微分方程、泛函分析、变分法和拓朴学的某些部分。同样对经典物理学——牛顿力学和电磁学作了较深入的讨论。其目的则是引导学生去重新审视和整理自己已...
程、泛函分析、变分法和拓扑学的某些部分口同样对经典物理学—牛顿力学和电磁学作了较深入的讨论。其 目的则是引导学生去重新审视和整理自己己学过的数学知识,并为学习新的数学知识—例如数学物理做准 备。 本书...
重温微积分 - 齐民友
我们以一种符合连续有效场论(CEFT)精神的方法分析最简单的小希格斯(SLH)模型的标量势。 通过要求使用125 GeV希格斯玻色子进行正确的电弱对称破坏(EWSB),我们能够得出假轴质量mη与重顶部质量mT之间的关系,这...
什么是数学!用于数学科普、重温复习的经典著作!精心排版!公式、插图都十分精美。
用图片重温历史:1995年的互联网是这样子的.docx
同学聚会PPT模板:欢乐时光重温.pptx
重温微积分前四章重排版齐民友.pdf
20190407-国泰君安-通信设备及服务行业:重温传统视频会议的三生三世,揭示云视频行业的十里桃花.pdf
微积分是科学与技术的基础。 本书对微积分起源、发展,特别是由于需求对微积分发展的推动,进行了重温。
重温老三篇心得体会精选13篇.doc
与真正的百科(例如维基百科)不同的是,《小时物理百科》系列更偏向于教材而不仅仅是一本供专业人士查阅的工具书.本书的主要面向的人群是: 1. 具有一定的高中数学物理基础,但没有上过任何大学数理课程,想自学...
半导体物理和器件:Lecture IV 重温量子力学.pdf
这项工作通过非弹性碰撞理论提出了关于俄歇效应的文章。 计算了一些分子的俄歇谱带所发射的电子的能量,以测试模型。
对于学过一点微积分知识的同学都可以尝试读一读,如果是数学专业的就更好地回味一下实分析的发展。
经典玩法:完美还原贪吃蛇的经典玩法,让玩家重温童年回忆。 易于上手:简洁直观的操作方式,玩家只需使用键盘W、A、S、D键即可控制贪吃蛇的移动。 高度可定制:源码结构清晰,方便开发者根据需求进行扩展和修改,...
大师之作,Martin Fowler的持续集成,中文版。持续集成是一种软件开发实践,在实践中项目成员频繁地进行集成,通常每个成员每天都会做集成工作,如此,每天整个项目将会有多次集成。