1、同余(合同式)
两个整数a,b,若它们除以正整数m所得的余数相等,则称a,b对于模m同余
记作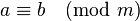
例如1≡13 (mod 12),可以理解为时钟上1点和13点的指针位置相同
重要性质

例如1^5=1,13 ^5=371293=30941*12+1
即1^5≡1≡13 ^5(mod 12)
2、欧拉函数(Euler's totient function)
欧拉函数 φ(n)是少于或等于n的数中与n互质的数的数目,例如φ(9) = 6,因为比9小的数中与9互质的有1, 2, 4, 5, 7,8六个数,所以9的欧拉函数为6。
计算方法:
将n分解为质数相乘的形式
 ,每个pi都是质数
,每个pi都是质数
则欧拉函数
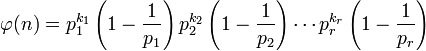
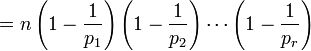
例如

两条结论
若n为质数,则φ(n)=n-1
若m与n互质,则 φ(mn) = φ(m)φ(n)
3、费马小定理与欧拉定理
费马小定理
若a为整数,p为质数则
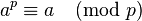
如果a不是p的倍数,可写为

推广:欧拉定理
对任何两互质正整数a, m, ,有
,有

4、模反
a的模反(模m)即满足下列等式的x
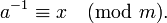
或写成
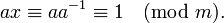
例如

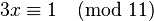
当x=4时上式成立,所以4是3的模反,
注意:4并不是唯一的解,在4的基础上加上模(11)的倍数依然满足上式,例如15,26,37,48等
但是寻找这样的x并不是一目了然,可以用下面的扩展欧几里得算法。
5、扩展欧几里得算法
作为欧几里得算法的扩展,寻找的是满足
ax + by = gcd(a,b)的x和y。
当a,b互质时,可以看出x是a在b模下的反(ax=1(mod y)) ;可以看出y是b在a模下的反(by=1(mod x))
我用python写了一个递归实现
运行实例,还是拿上面的例子,求3在模11下的反
得到结果:
意即4*3+(-1)*11=1
因此可得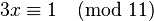 的解为4
的解为4
6、密钥生成
选取两个素数p和q
计算n=pq
计算φ(n) = (p – 1)(q – 1)
(可由2中的两个结论推出)
选取e使得
1 < e < φ(n)且e与φ(n)互质,e和n作为公钥
计算 d =
e–1 mod φ(n); d和n作为密钥
7、加密
将公钥(n,e)传送给对方,自己保留密钥。对方对明文进行加密。
明文m,密文c,由密钥(n,e)可得
c = me (mod
n).
8、解密
收到对方传过来的密文c后可以用密钥(d,n)进行解密,得到明文m
m = cd (mod
n).
9、实现
用python把流程走一遍
分享到:





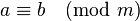

 ,每个pi都是质数
,每个pi都是质数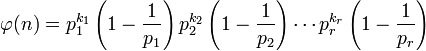
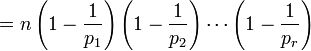

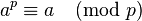

 ,有
,有
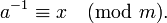
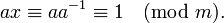

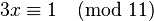



相关推荐
RSA算法演示RSA算法演示RSA算法演示RSA算法演示RSA算法演示RSA算法演示RSA算法演示RSA算法演示RSA算法演示RSA算法演示RSA算法演示
RSA加密算法实例,介绍了RSA的几种实例的实现方式
RSA算法工具RSA算法工具RSA算法工具RSA算法工具 RSA算法工具
RSA实现算法报告关于RSA算法的实现代码
VC++实现RSA算法
RSA加密算法介绍,密匙的求解过程讲解,密匙的求解实例分析。
RSA算法RSA算法RSA算法RSA算法RSA算法RSA算法RSA算法RSA算法RSA算法
本例介绍了RSA算法加密,内有详细的算法说明及实例,对研究加解密算法的人很有帮助
RSA算法演示.rar
rsa加密算法实例
RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但是想要...RSA是被研究得最广泛的公钥算法,从提出到现今的三十多年里,经历了各种攻击的考验,逐渐为人们接受,普遍认为是目前最优秀的公钥方案之一。
提供了rsa算法的java类及测试代码.其中已经用过,有需要的可以拿去
易语言RSA算法演示源码,RSA算法演示
MFC界面 相当于一个用RSA算法实现的加密小软件
RSA算法C++实现 RSA算法C++实现
RSA算法和RSA数字签名算法的实现,RSA算法和RSA数字签名算法的实现,RSA算法和RSA数字签名算法的实现
RSA签名算法实例,使用RSA的SignHash和VerifyHash可以同样做到SignData和VerifyData,事实上还有一种方法进行公钥加密的签名 认证。就是.NET中的AsymmetricSignatureFormatter和AsymmetricSignatureDeformatter。直 ...
RSA算法的纯Python实现,压缩包内共4个文件,分别是 1、大整数的运算库(当然不是算加减乘除的,这个python本身就有)。这个库是计算乘模运算,幂模运算(蒙哥马利算法),最大公约数算法及扩展最大公约数算法(扩展...
用实例讲解RSA加密算法(精)
目前的公开密钥算法大部分基于大整数分解、有限域上的离散对数问题和椭圆曲线上的离散对数问题,这些数学难题的构建大部分都需要生成一种超大的素数,尤其在经典的 RSA算法中,生成的素数的质量对系统的安全性有很大...