小波变换网文精粹:小波变换教程(六)
原文:ROBI POLIKAR. THE ENGINEER'S ULTIMATE GUIDE TO WAVELET ANALYSIS:The Wavelet Tutorial
网址:http://users.rowan.edu/~polikar/WAVELETS/WTtutorial.html
译文转自:http://blog.163.com/renfengyuee@126/blog/static/3594313620109117185720/
六、小波变换基础:傅立叶变换(一)
让我们对前面的内容做个简要回顾。
基本上,我们要用小波变换来处理非平稳信号,即那些频率分量随时间变换而变换的信号。上文我已经说过傅立叶变换不适合处理这些非平稳信号,并且举了例子来来佐证。再做一个快速的回顾吧,看下面这个例子:假定我们有两个不同的信号,再假设他们都有相同的频谱分量,只有一点不同,其中一个信号含有的四个频率分量在整个信号周期内都存在,另外一个也有相同的四个频率分量,但出现的时间各不相同。两个信号的傅立叶变换将会是一样的,如同在文章的第一部分中所讲到的那个例子。虽然这两个信号是完全不同的,但他们的傅立叶变换却是相同的!这一点很明显告诉我们不能用傅立叶变换来处理非平稳信号。但是这是为什么呢?换句话说,为什么完全不同的两个信号却有同样的傅立叶变换呢?傅立叶变换到底是怎么变换的?
信号处理中的一个重要里程碑:傅立叶变换!!
基于以下两个原因,我不想深究傅立叶变换的细节:
1、 这个课题对本教程来说太广了。
2、 它不是我们主要关注的对象。
不过,基于以下原因,我将会在文中涉及一些要点:
1、 为了理解小波变换,你需要傅立叶变换作为背景知识。
2、 它是到目前为止最重要的信号处理工具,已经被用了很多很多年了。
在十九世纪年(或许是1822年,不过你并不需要知道这么确切的时间,相信我,绝对比你能想起来的时间还早得多),法国数学家傅立叶,发现所有周期信号都可以表示为无限的周期复指数函数的和。在他发现了这个著名的周期函数性质之后,其想法被推广到第一个非周期函数,然后是周期和非周期的离散信号。在这之后,傅立叶变换就成了在计算机中非常适合的计算工具。年,出现了一个叫做快速傅立叶变换的新算法,从此傅立叶变换更加流行了。
傅立叶变换将信号分解为具有不同频率的复指数函数,可以用以下两个公式来解释它的变换过程:
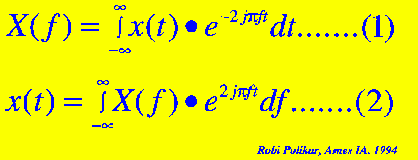
图2.1
在上式中,表示时间,表示频率,表示要分析的信号。注意到表示信号的时域,表示信号的频域,这个约定用来区别对信号的两种表示。公式叫做x(t)的傅立叶变换,公式叫做X(f)的傅立叶逆变换,其结果是。用过傅立叶变换的人对这些已经很熟悉了,但不幸的是,很多人虽然用到了这些公式,却没有理解它的基本原理。现在仔细看公式:信号是一些指数项的累加和,每个项对应特定的频率,然后在整个时域内整合起来(这里的“整个时域”将在下面进行介绍)。公式中的指数项还可以被写成下面这样:
cos(2.pi.f.t)+j.Sin(2.pi.f.t).......(3)
上面的表达式以一个频率为的余弦信号作为实部,一个频率为的正弦信号作为虚部。所以我们实际要做的是用一些复数表达式叠加出原始信号,这些复数表达式包含了频率为的正弦和余弦分部。然后我们对乘积积分,即我们把乘积中的所有的点叠加起来。如果积分结果(只不过某种无限求和)的值很大,那么我们可以这样说:信号x(t)在频率f处有一个大的频谱分量。信号主要是由频率为的分量组成。如果积分结果的值较小,就意味着信号中频率为的分量很少。如果积分结果为,表明信号中根本不存在频率为的分量。这里很有意思,让我们看看积分是怎么回事:信号是由一些不同频率的正弦项叠加起来的,如果信号中频率为f的分量幅值较大,那么这个分量就和正弦项重叠,他们的积就会(相对)较大,这表明信号x有一个频率为f的主要分量。
不过,如果信号中不含频率为的分量,则乘积结果为,这表明信号没有频率为的分量。如果频率为的分量不是信号的主要组成部分,则乘积会(相对)较小。这就说明频率为f的分量在信号中的幅值很小,不是信号中的主要组成分量。现在,变换公式中的积分方式已经有些过时了。公式中左边是一个对频率的函数,因此,式的积分是由每一个频率值计算出来的。
注意!!因为积分是从负无穷到正无穷,所以积分在所有时间内有效。这说明了不管频率为的分量何时出现,都将会影响积分结果。换句话说,不管频率为的分量出现在时刻还是,都将对积分结果产生相同的影响。这就是为什么傅立叶变换不适合分析随时间变化,频率改变的信号,即非平稳信号。当且仅当频率为的分量一直存在(对所有的),傅立叶变换得到的结果才有意义。傅立叶变换可以给出某个频率分量存在与否,其结果不取决于信号出现的时间。需要知道的是,一个平稳的信号才优先用傅立叶变换进行处理。第一部分中给出的例子现在已经讲得很明白了,这里我再次给出:看下式:
x(t)=cos(2*pi*5*t)+cos(2*pi*10*t)+cos(2*pi*20*t)+cos(2*pi*50*t)
信号中含有四个频率分量,所有分量在信号的整个周期内都存在。
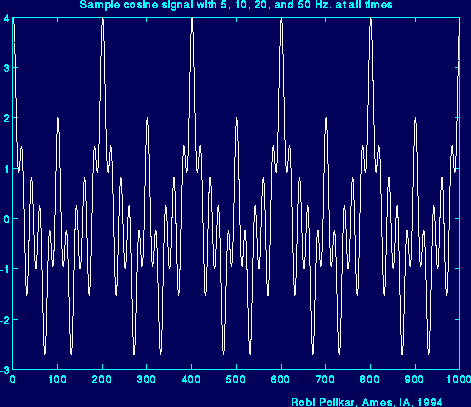
图2.2
这里是它的傅立叶变换。频率轴被剪切过了,因为理论上来说它是无穷的(仅指连续傅立叶变换,实际上我们在这里做的是离散傅立叶变换,频率轴最少要达到采样频率的两倍处,变换过的信号是对称的。不过现在这些都不重要)。

图2.3
上图中出现了四个尖峰,对应四个不同的频率。
PS:原文pdf打包下载地址:http://download.csdn.net/detail/deepdsp/4061006
分享到:




相关推荐
UML精粹:标准对象建模语言简明指南-带目录 UML精粹:标准对象建模语言简明指南-带目录 UML精粹:标准对象建模语言简明指南-带目录
清华大学出版社《UML精粹:标准对象建模语言简明指南 第3版 》在紧迫的时间压力下 程序员很难通过紧跟技术创新的脚步来享受软件工程领域的最新成果 正因如此 殿堂级大师Martin Fowler这本旨在帮助专业人士提升效率的...
微软四大名著之编程精粹:编写高质量C语言代码。亚马逊评出的微软四大名著之一,经典。
UML的大作.英文原版,CHM格式。个人觉得比较实用,可做手册速查
UML精粹:标准对象建模语言简明指南.pdf 本书为Martin Fowler所著《UML精粹》一书第3版之中译本。原书首版自1997年问世以来,深受读者欢迎,堪称书中上乘。
CMMI精粹:集成化过程改进实用导论
Excel实战技巧精粹:Excel模板1000例
信息系统开发实例精粹:讲了六个例子,运输的 宾馆的 学生的 ……
诚意推荐《MySQL面试精粹:90%场景题深度剖析》,一本专为数据库从业者量身定制的实战宝典。这本书籍涵盖了超过90%的MySQL面试高频场景题,以其深度剖析和详尽解答,引领你穿越复杂的技术丛林,直抵MySQL知识的核心...
注意:这个可是最新英文版的,要学的话需要点英文基础哦! ......解压密码 www.infoxa.com
GPU编程 GPU精粹:GPU 3D和通用编程技巧
AXURE RP8实战手册 网站和APP原型制作案例精粹:全选与取消全选效果.rp
AXURE RP8实战手册 网站和APP原型制作案例精粹:制作商品列表.rp
HTML5精粹:利用HTML5开发令人惊奇的Web站点和革命性应用
AXURE RP8实战手册 网站和APP原型制作案例精粹:拖动滑块解锁.rp
Excel实战技巧精粹:Excel实用模板972例:个体工商户设立登记申请书.xls中介单位人员登.xls中外学者越洋对话日程安排.xls中央基层预算单位开立银行帐户申请表.xls中央基层预算单位财政支出月报表.xls中学校小升初...
AXURE RP8实战手册 网站和APP原型制作案例精粹:商品列表价格排序.rp