差分约束:线性规划矩阵A的每一行包含一个1与一个-1,其他元素为0.因此,由Ax<=b给出的约束条件是m个差分约束集合,其中包含n个未知元。每个约束条件为不等式:
xj-xi<=bk
其中1<=i,j<=n,i<=k<=m
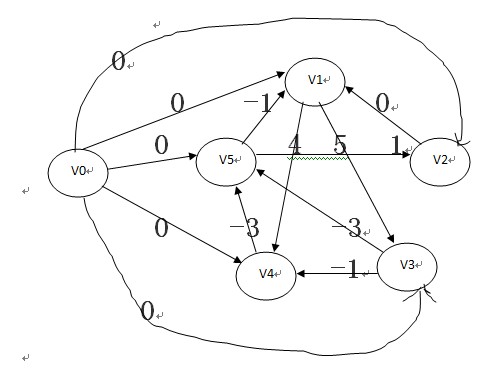
解决方法:把n个未知元看成n的有向图的顶点,xj-xi<=bk表示顶点j到顶点i长度为bk的有向线段。再添加一个v0顶点,与v0到其余顶点的有向线段,长度为0。(如下图)
可以证明 xi=β(v0,vi)(β(v0,vi)为顶点0到顶点i的最短路径长度)。所以就可以利用Bellman_Ford算求单源最短路径(不能用Dijkstra算法,因为有向线段长度可以为负)
// 差分约束系统.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include<iostream>
#define MAX 100
#define Infinity 65535
using namespace std;
//边的尾节点结构体
struct edgeNode
{
int no; //边尾端的序号
int weight; //边权值
struct edgeNode * next; //下一个
};
//节点结构体
struct vexNode
{
char info; //节点名称
struct edgeNode *link; //与之相连的端点
};
//存储节点信息
vexNode adjlist[MAX];
//前驱节点
int parent[MAX];
////源点到节点j最短路径的花费
int lowcost[MAX];
//差分矩阵
int a[MAX][MAX];
//约束集
int w[MAX];
//根据差分矩阵建立邻接表存储
//adjlist为节点集,parent[j]为从0节点到节点j的最短路径的前驱节点
//lowcost[j]为从0节点到节点j的最短路径的代价
//w为输入的差分约束
//m,n分别为差分矩阵的行数和列数
void createGraph(vexNode *adjlist,int *parent,int *lowcost,int *w,int m,int n)
{
int i,j;
//初始化,节点vi的名称为char(a+i)
for(i=0;i<=n;i++)
{
adjlist[i].info = (char)('a' + i);
adjlist[i].link = NULL;
lowcost[i] = Infinity;
parent[i] = i;
}
int col1,col2;
col1 = col2 = 0;
edgeNode *p1;
for(i=1;i<=m;i++)
{
for(j=1;j<=n;j++)
{
if(a[i][j]==-1)
col1 = j;
else if(a[i][j]==1)
col2 = j;
}
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = col2;
p1->weight = w[i];
p1->next = adjlist[col1].link;
adjlist[col1].link = p1;
}
for(i=1;i<=n;i++)
{
p1 = (edgeNode*)malloc(sizeof(edgeNode));
p1->no = i;
p1->weight = 0;
p1->next = adjlist[0].link;
adjlist[0].link = p1;
}
lowcost[0] = 0;
}
//寻找v0到,每一个节点的最短路径
bool Bellman_Ford(vexNode *adjlist,int *lowcost,int *parent,const int n)
{
int i,j;
for(j=0;j<n;j++)
{
for(i=0;i<=n;i++)
{
edgeNode *p1 = adjlist[i].link;
while(p1 != NULL)
{
if(lowcost[i]+p1->weight <lowcost[p1->no])
{
lowcost[p1->no] = lowcost[i]+p1->weight;
parent[p1->no] = i;
}
p1 = p1->next;
}
}
}
//检查有无负回路
for(i=1;i<=n;i++)
{
edgeNode *p2 = adjlist[i].link;
while(p2 != NULL)
{
if(lowcost[p2->no]>lowcost[i]+p2->weight)
return false;
p2 = p2->next;
}
}
return true;
}
int _tmain(int argc, _TCHAR* argv[])
{
int cases;
cout<<"请输入案例的个数:";
cin>>cases;
while(cases--)
{
int i,j;
int n,m;
cout<<"请输入差分矩阵的行数(m)与列数(n):";
cin>>m>>n;
cout<<"请输入差分矩阵:"<<endl;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
cin>>a[i][j];
cout<<"请输入约束集:"<<endl;
for(i=1;i<=m;i++)
cin>>w[i];
//创建邻接表
createGraph(adjlist,parent,lowcost,w,m,n);
//输出邻接表
/*
for(i=0;i<=n;i++)
{
edgeNode *p = adjlist[i].link;
cout<<i<<":";
while(p != NULL)
{
cout<<"("<<p->no<<","<<p->weight<<") ";
p = p->next;
}
cout<<endl;
}
*/
//调用Bellman-Ford算法
bool flag = Bellman_Ford(adjlist,lowcost,parent,n);
if(!flag)
cout<<"无解"<<endl;
else
{
//输出解集
cout<<"其中一个解集为(此解集加上一个任意的常数d也是其解集):"<<endl;
for(i=1;i<=n;i++)
cout<<"x"<<i<<"="<<lowcost[i]<<endl;
}
}
system("pause");
return 0;
}
---------------------------------------------------程序测试---------------------------------------------------

请输入案例的个数:1
请输入差分矩阵的行数(m)与列数(n):8 5
请输入差分矩阵:
1 -1 0 0 0
1 0 0 0 -1
0 1 0 0 -1
-1 0 1 0 0
-1 0 0 1 0
0 0 -1 1 0
0 0 -1 0 1
0 0 0 -1 1
请输入约束集:
0 -1 1 5 4 -1 -3 -3
其中一个解集为(此解集加上一个任意的常数d也是其解集):
x1=-5
x2=-3
x3=0
x4=-1
x5=-4
请按任意键继续. . .
分享到:











相关推荐
差分约束系统是一种用于处理线性不等式约束的数学模型,主要应用于寻找变量之间的最大或最小差值。在这个系统中,我们有n个变量x[0], x[1], ..., x[n-1]和m个...在C++编程中,实现这些算法可以高效地处理差分约束系统。
在本项目中,我们将探讨如何利用C++编程语言和Visual Studio 2013开发环境来实现差分进化算法,以求解平方和函数的最小值问题。 平方和函数通常定义为所有变量平方和的总和,即f(x) = Σ(xi^2),其中x是包含多个...
标题中的“OPENCV视频检测车流量(帧间差分法)_同时检测4路车道_C++”表明这是一个基于OpenCV库的C++程序,用于实时监测和计算视频中多车道的车辆流量。此方法主要利用帧间差分技术来识别车辆的移动。以下是关于这个...
有限差分声波方程正演是地球物理勘探领域中常用的一种模拟技术,主要用于研究地下结构的波动特性。在这个程序中,我们利用MATLAB这一强大的数值计算环境来实现这一复杂的过程。MATLAB因其丰富的数学函数库和易于编程...
总结来说,这个压缩包包含了一个使用Visual C++实现的程序,该程序使用SPFA算法解决了差分约束系统的问题,这在ACM竞赛中是一个常见的算法挑战。通过分析“chafenyueshu.txt”文件,我们可以深入理解如何利用图论...
本文主要探讨了两种常用的方法:背景差分法和邻帧检测法,并结合OpenCV库以及Visual C++ 2008环境进行实现。下面将详细阐述这两种方法以及OpenCV和VC2008的应用。 背景差分法是视频分析中常用的一种技术,主要用于...
10. **C++编程实践**:书中会强调如何高效地用C++实现这些算法,包括模板、面向对象编程、STL(标准模板库)的使用,以及内存管理和性能优化。 11. **并行计算**:随着多核处理器的普及,书中可能也会提及如何利用...
在OpenCV中,可以找到实现OSTU算法的函数,便于开发者快速构建背景差分系统。 标签中的"opencv"强调了使用OpenCV进行实现,"算法"和"人工智能"进一步揭示了这是涉及机器学习和智能决策的领域。"计算机视觉"则明确了...
2. **前向差分**:计算两帧间的像素差异,作为光流的初始估计。 3. **光流方程**:基于Lucas-Kanade方法或Horn-Schunck方法求解光流,这些方法试图最小化相邻像素的亮度变化。 4. **优化**:通过迭代过程优化初始...
**C++实现LSSVM(线性可分支持向量机)** 支持向量机(Support Vector Machines,SVM)是一种强大的监督学习算法,广泛应用于分类和回归问题。线性可分支持向量机(Linearly Separable Support Vector Machines,...
这篇文档主要讨论的是如何用C++实现SMO算法。 首先,我们看到代码中定义了一个名为`SMO`的类,这个类包含了SVM模型的训练和预测所需的基本组件。类的构造函数初始化了一些关键参数,如样本数量(`N`),特征维度(`...
高速信号通常需要采用差分对或屏蔽线来减小噪声影响。 3. **电源和地线**:电源和地线的布设对电路性能至关重要。通常采用大面积覆铜作为电源平面和地平面,以降低阻抗,提供良好的电磁屏蔽。 4. **层叠设计**:...
这本书深入探讨了使用C++编程语言实现数值计算的方法和技术,对于理解和应用数值方法在解决实际问题中具有重要的指导意义。 1. **数值计算基础** - 数值方法是处理数学问题的一种近似方法,尤其适用于不能获得解析...
差分演化算法(Differential Evolution, DE)是一种基于群体智能理论的优化算法,源自1995年Storn等人提出的方法,最初应用于切比雪夫多项式问题,后来因其高效性和鲁棒性,成为解决复杂优化问题的重要工具。...
差分约束系统(Differential Constraint System,DCS)是一种数学模型,常用于解决优化问题,如旅行商问题、调度问题等。在这个上下文中,这些题目可能要求参赛者或学生使用差分约束来解决问题。 标签“ad6crack.r ...
1. "POJ1716-Integer Intervals【Difference Constraints】.cpp":这可能是基于差分约束系统理论的C++代码实现,它可能采用了动态规划或者线性规划的方法来解决问题。 2. "POJ1716-Integer Intervals【Greed】.cpp...
《常用数值算法与程序(C++版)》是由何渝编著的一本经典书籍,它主要涵盖了数值计算领域中常见的算法及其C++实现。数值计算是计算机科学中的一个重要分支,涉及许多实际问题的求解,如工程计算、物理模拟、数据分析...
3. **全局优化**:提供了一些全局优化算法,如模拟退火、遗传算法、差分进化、直接搜索方法等。 在 NLopt-2.3 中,你可以期待以下内容: - **源代码**:库的核心实现,包括算法的实现和接口定义。 - **头文件**(`...
《科学与工程数值计算算法(Visual C++版)》这本书提供了许多数值计算方法的C++实现,旨在帮助读者理解并掌握数值方法在实际问题中的应用。 首先,数值分析是数学的一个分支,主要研究如何用计算机来近似解决数学...
对于初值问题,还可以使用隐式和显式差分格式。 4. **优化算法**:数值分析中的优化问题通常涉及找到函数的最小值或最大值。C++中常见的优化算法有梯度下降法、牛顿法、拟牛顿法(如BFGS和L-BFGS)、共轭梯度法等。...