// 最优二叉查找树的期望搜索代价.cpp : Defines the entry point for the console application.
//
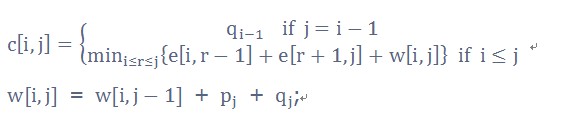
#include "stdafx.h"
#include<iostream>
#include<cmath>
#include<limits>
#define N 100
using namespace std;
const double MAX = numeric_limits<double>::max(); //double的最大值
int _tmain(int argc, _TCHAR* argv[])
{
//p[j]存储第j关键字的概率(j=1...n)
double p[N];
//存储第j虚拟键的概率(j=0...n)
double q[N];
//存储包含关键字ki....kj的最优子树的搜索代价
double c[N][N];
//存储包含关键字ki....kj和虚拟键的最优子树的概率和
double w[N][N];
//存储存储包含关键字ki....kj的最优子树的根
int root[N][N];
int cases;
cout<<"请输入案例的个数:"<<endl;
cin>>cases;
while(cases--)
{
int n;
double sum = 0;
int i,j,l;
cout<<"请输入关键字的个数:"<<endl;
cin>>n;
cout<<"请输入每个关键字的概率:"<<endl;
for(i=1;i<=n;i++)
{
cin>>p[i];
sum += p[i];
}
cout<<"请输入每个虚拟键的概率:"<<endl;
for(i=0;i<=n;i++)
{
cin>>q[i];
sum += q[i];
}
//
if(abs(sum-1)>0.01)
{
cout<<"输入的概率和不为1,请重新输入"<<endl;
cases++;
continue;
}
for(i=1;i<=n+1;i++)
{
c[i][i-1] = q[i-1];
w[i][i-1] = q[i-1];
}
for(l=1;l<=n;l++)
{
for(i=1;i<=n-l+1;i++)
{
j = l+i-1;
c[i][j] = MAX;
w[i][j] = w[i][j-1] + p[j] +q[j];
int r;
for(r=i;r<=j;r++)
{
double k = c[i][r-1] + w[i][j] + c[r+1][j];
if(k<c[i][j])
{
c[i][j] = k;
root[i][j] = k;
}
}
}
}
cout<<"最优二叉查找树的期望搜索代价为:"<<c[1][n]<<endl;
}
system("pause");
return 0;
}
---------------------------------------------测试程序----------------------------------------------
请输入案例的个数:
1
请输入关键字的个数:
5
请输入每个关键字的概率:
0.15 0.10 0.05 0.10 0.20
请输入每个虚拟键的概率:
0.05 0.10 0.05 0.05 0.05 0.10
最优二叉查找树的期望搜索代价为:2.75
请按任意键继续. . .
分享到:






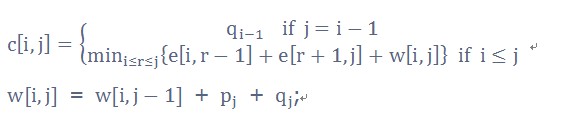



相关推荐
用C++实现的最优二叉查找树,简单,明了,是数据结构里经典必学算法,初学者适用
c语言实现的用动态规划实现最优二叉查找树,,,具体参见附件,2.txt中的内容为: 5 0.15 0.10 0.05 0.10 0.20
总之,这个C++课程作业通过动态规划法实现了最优二叉查找树的构建,旨在提高搜索效率。通过分析和理解代码,你可以深入学习动态规划的应用以及二叉查找树的优化策略。对于学习数据结构和算法的学生来说,这是一个很...
使用C++实现最优二叉查找树,对正在学习算法的同学应该挺有帮助的
在这个问题中,我们用C#语言实现了动态规划算法来构建最优二叉搜索树。动态规划是一种解决最优化问题的有效方法,它将大问题分解为小问题,然后通过构建子问题的最优解来获得原问题的最优解。 首先,我们需要理解...
下面是一个简单的C++代码示例,展示了如何根据上述步骤实现最优二叉搜索树的构建过程: ```cpp #include #include using namespace std; const int MaxN = 50; int a[MaxN]; // 访问概率 int b[MaxN]; // 外部...
在C++中实现二叉查找树,我们需要定义一个结构体或类来表示树节点,包括节点的值、指向左子节点和右子节点的指针。以下是一个简单的C++实现框架: ```cpp struct TreeNode { int val; TreeNode* left; TreeNode*...
在C++中实现二叉查找树,一般会定义一个结构体或类来表示树节点,包括键、值和子节点指针。然后,提供一系列成员函数来执行基本操作,如`insert`(插入)、`search`(查找)、`delete`(删除)。以下是C++实现二叉...
在C++编程中,二叉查找树(Binary Search Tree,简称BST)是一种常见的数据结构,它具有以下特性:对于任意节点,其左子树中的所有节点的值都小于该节点的值,右子树中所有节点的值都大于该节点的值。这种性质使得...
14.3 二叉搜索树的操作和实现 14.3.1 类binarySearchTree 14.3.2 搜索 14.3.3 插入 14.3.4 删除 14.3.5 二叉搜索树的高度 14.4 带有相同关键字元素的二叉搜索树 14.5 索引二叉搜索树 14.6 应用 14.6.1 直方图 14.6.2...
C++实现二叉查找树时,通常会定义一个结构体或类来表示树的节点,包括键值、左右子节点的指针。例如: ```cpp struct TreeNode { int key; TreeNode* left; TreeNode* right; }; ``` 在C++中,二叉查找树的基本...
设S=(x1,x2,…,xn)是有序集,且x1…,已知键值和区间的存取概率分布为(a0,b1,a1,b2,…,bn,an),其中ai表示相应区间的搜索概率,bi表示相应键值的...在所有表示有序集的二叉树中找出一棵具有最小平均路长的二叉搜索树
使用二叉链表和c++来实现二叉搜索树,提供插入、删除、遍历、求最小节点、最大最节点等操作。
在"二叉查找树实现简单的信息检索"中,我们关注的是如何利用二叉查找树来高效地检索信息。首先,我们需要创建一个二叉查找树的数据结构。在提供的文件中,`Binary_tree.h`和`Binary_tree.cpp`很可能是定义和实现这个...
资源内容:完整的二叉查找树C++头文件,包括运算符重载,bst类构造器、bst类析构器、destroy()、size()、insert(),迭代器类的声明与实现,++运算符重载(前置、后置)、--运算符重载、*运算符重载、!=运算符重载、...
### C++ 实现二叉查找树 #### 一、引言 本文将详细介绍如何使用C++来实现一个二叉查找树(Binary Search Tree, BST),包括其基本操作:插入、删除、遍历等,并通过示例代码进行解释。二叉查找树是一种非常重要的数据...
二叉查找树的常用操作,含C++代码,找工作的时候可以放在手机里看。
在C、C++和Java这三种编程语言中实现二叉查找树,主要涉及以下几个关键操作: **插入操作:** - 首先,从根节点开始,比较新节点的键值与当前节点的键值。 - 如果新节点的键值小于当前节点,移动到当前节点的左子树...
### 二叉查找树的C++实现 #### 一、二叉查找树简介 二叉查找树(Binary Search Tree),也称作有序或排序二叉树,是一种特殊的二叉树数据结构,其每个节点包含一个键(key)和两个指针(指向左子树和右子树)。对于...